Biomechanics expert Dr. John Lloyd has served attorneys nationwide for 25+ years in biomechanics, human factors, helmet testing and motorcycle accident expert
Dr. Lloyd is a distinguished authority in motorcycle accident reconstruction and human factors analysis, with decades of experience. His understanding of the unique dynamics involved in motorcycle crashes sets him apart as a true specialist in the field.
Dr. Lloyd spent his career as a senior researcher at the VA Hospital in Tampa, FL, serving as Director of the Biomechanics Research Laboratory and Director of the Traumatic Brain Injury Research Laboratory. In addition he held a courtesy faculty appointment as Assistant Professor in the University of South Florida College of Engineering from 2002-2022, and is currently the Research Director of BRAINS, Inc.
To date, Dr. Lloyd’s work has been published in six book chapters and 33 peer-reviewed journals, as well as presented at more than 100 national and international conferences (see curriculum vitae).
Comprehensive Approach
Dr. Lloyd goes beyond the obvious and delves deep into the technical intricacies of each case. As a multi-disciplinary expert he combines, accident reconstruction, biomechanics and human factors to provide a holistic view of the accident, ensuring no detail goes unanalyzed.
Accurate Motorcycle Crash Reconstructions
Using state-of-the-science reconstruction tools and real world data, Dr. Lloyd meticulously creates 3D accident reconstructions with unparalleled accuracy. This empowers him to provide precise insights into the sequence of events leading up to the incident.
Human Factors Insight
Understanding the role of human behavior is crucial in accident analysis. Dr. Lloyd’s human factors expertise allows him to investigate the cognitive factors affecting both motorcycle riders and automobile drivers, offering invaluable insights into decision-making processes.
Courtroom Excellence
Dr. Lloyd’s reputation as a credible and authoritative expert makes him an invaluable asset in the courtroom. He excels at conveying complex technical information to the jury in an accessible manner, helping you present a compelling case, backed by robust scientific analysis.
To date, Dr. Lloyd has provided expert witness Deposition and Trial Testimony in more than 160 civil and criminal cases. His expertise in motorcycle crashes, motorcycle riding and operation, helmet protection, biomechanics and human factors has been recognized by courts across the United States and Internationally. The analysis methods that Dr. Lloyd utilizes are published in peer-reviewed scientific journals.
Unquestionable Expert Integrity
Ethics and integrity are the cornerstones of our practice. You can trust that our analyses are unbiased, objective and founded on the highest standards of professionalism.
Alabama Alaska Arizona Arkansas California Colorado Connecticut Delaware Florida Georgia Hawaii Idaho Illinois Indiana Iowa Kansas Kentucky Louisiana Maine Maryland Massachusetts Michigan Minnesota Mississippi Missouri Montana Nebraska Nevada New Hampshire New Jersey New Mexico New York North Carolina North Dakota Ohio Oklahoma Oregon Pennsylvania Puerto Rico Rhode Island South Carolina South Dakota Tennessee Texas Utah Vermont Virginia Washington West Virginia Wisconsin Wyoming
The following is a peer-reviewed article on Motorcycle Accident Reconstruction, which was originally published in the Journal of Forensic Biomechanics in January 2016.
Corresponding author: John D Lloyd, Research Director, BRAINS, Inc., 32824 Michigan Avenue San Antonio, Florida, 33576, USA, Tel: 813-624-8986; Fax: 352-588-0688; E-mail: drjohnlloyd@tampabay.rr.com
Abstract
In a motorcycle accident, the motorcycle and rider typically become independent, each following their own path to final rest. Consequently, the biomechanical analysis of a motorcycle accident reconstruction is complex. A biomechanical model to assess rider kinematics associated with motorcycle accidents is presented, which may be important to forensic scientists involved in the analysis of such events. This model can also be applied to other activities, including cycling, equestrian sports, skiing, skating, running, etc.
In a motorcycle accident reconstruction, it is first important to understand the mechanisms by which a rider may be ejected from their motorcycle and how drag factors affect the motorcycle and rider independently. Next we determine rider trajectory, taking into consideration rider anthropometry and posture, results from which are used to derive impact velocity as a function of linear and angular components. A case study is presented, demonstrating how the presented model can be applied to a collision involving a single motorcycle.
Introduction to Motorcycle Accident Reconstruction
Motorcycles are a luxury in the developed world, where they are used mostly for recreation. Whereas in developing countries, motorcycles are required for utilitarian purposes due to lower prices and greater fuel economy. It is estimated that in 2016 there will be more than 134 million motorcycles worldwide [1], 60-80% of which are in the Asia Pacific and Southern and Eastern Asia regions. In 2011 there were more than 8.2 million registered motorcycles in the United States [2], representing 3% of all US registered vehicles, with California, Florida and Texas leading the number of motorcycles per state [3].
3.1. Epidemiology of motorcycle accidents
In the United States motorcyclists travelled 18.5 billion miles in 2011, which represents only 0.6% of total vehicle miles travelled, yet motorcyclists accounted for 14% (4,612) of traffic fatalities and 4% (81,000) of all occupant injuries [2]. According to the U.S. National Highway Traffic Safety Administration (NHTSA), when compared with automobiles, per vehicle mile traveled, motorcyclists’ risk of a fatal crash is 35 times greater than that of a car occupant [4].
Two major epidemiologic studies into the causation of motorcycle accidents have been conducted in North America and Europe: the Hurt Report and the MAIDS report. The Hurt Report [5] showed that failure of motorists to detect and recognize motorcycles in traffic is the prevailing cause of motorcycle accidents. Seventy-five percent of accidents were found to involve a motorcycle and a passenger vehicle, while the remaining 25% of accidents were single motorcycle accidents. Two-thirds of motorcycle-car crashes occurred when the car driver failed to see the approaching motorcycle and violated the rider’s right-of-way. Findings of the Hurt study indicate that severity of motorcyclist injury increase with speed, alcohol consumption, motorcycle size and speed.
The MAIDS study (Motorcycle Accidents In Depth Study) [6] is the most recent epidemiologic study of accidents involving motorcycles, scooters and mopeds, which was conducted in 1999 across five European countries to investigate motorcycle accident exposure data. Key findings show that passenger cars were the most frequent collision partner (60%), where 69% of the drivers report that they did not see the motorcycle and the predominance of motorcycle accidents (54.3%) occurred at an intersection.
In the United States alone, it is estimated that the total direct costs associated with motorcycle crashes in 2010 was approximately $16 billion. However, the US Government Accountability Office (GAO) predicts that full costs of motorcycle crashes are likely considerably higher because some difficult-to-measure costs, such as longer-term medical costs, are not included [7].
Biomechanical Model
A new model is presented for the purpose of investigating motorcycle accident reconstruction biomechanics involving a lone motorcycle, which accounts for 25% of all motorcycle-related accidents according to the Hurt report [5]. This model is unique in that it incorporates measures of rider anthropometry (body measurements) and riding posture, which have a direct effect on trajectory and overall height of the vertical component of the impact.
The model presented herein may be applied not only to motorcycle accidents, but also to a wide range of activities, including cycling, equestrian sports, skiing, skating, running, etc.
Methods
It is first important to understand the mechanisms by which a rider may be ejected from their motorcycle and how drag factors affect the motorcycle and rider independently. Next we determine rider trajectory, results from which are used to derive impact velocity as a function of linear and angular components. Finally, characteristics of the impact surface are considered with respect to impact accelerations.
5.1. Rider ejection
There are a number of ways that a rider can be ejected from the bike in a lone motorcycle accident. Two common ways of ejection are the lowside (Figure 1A) and highside (Figure 1B) crash. A rider may also be ejected over the handlebars (Figure 1C).
Figure 1 – Rider Ejected from Motorcycle
The lowsider or lowside is a type of motorcycle crash usually occurring in a turn (Figure 1A). A lowside crash is caused when either the front or rear wheel slides out as a result of either too much braking in a corner, too much acceleration through or out of a corner, or too much speed carried into or through a corner for the available traction. A lowside crash may also be caused by unexpected slippery or loose material (such as oil, water, dirt or gravel) on the road surface.
A highsider or highside is a type of motorcycle accident characterized by sudden and violent rotation of the motorcycle about its longitudinal axis. This generally happens when the rear wheel loses traction, skids, and then suddenly regains traction, creating a large torque, ejecting the rider off the side of the motorcycle, oftentimes head-first (Figure 1B).
Highside and lowside accidents differ as follows: during a lowside the rear wheel slips laterally and continuously until the motorcycle falls onto the side facing the inside of the corner.Whereas during a highside crash the rear wheel slips laterally before suddenly regaining traction and flipping the motorcycle toward the outside of the corner (the higher side of the motorcycle). Highsides happen quickly and are very violent consequently injuries tend to be more severe in a high side crash, compared to a lowside crash.
Endo, short for “end over end,” occurs when the front end of a motorcycle stays fixed while the rear rotates up into the air, causing a rider to fly over the handlebars (Figure 1C).
5.2. Drag factors
Drag factors for motorcycles have been established based on motorcycle accident reconstruction and typically range from 0.2-1.0 [8], where 0.25 represents a motorcycle with a fairing [9], such as a sport motorcycle. Sport and sport touring motorcycles will likely slide further than a cruiser-style motorcycle, which have more external components that resist sliding, for which a drag factor of 0.5 is commonly adopted Table 1, below, presents drag factors for street motorcycles sliding on typical road surfaces [10-13].
Table 1: Drag Factors for Sliding Motorcycles
Drag factors for the rider are typically higher than those for motorcycles sliding on a dry asphalt or concrete roadway. An extensive series of motorcycle accident reconstruction tests were carried out by the West Midlands Police in the United Kingdom in which they calculated the drag factor value of a crash-test dummy sliding across an airfield surface. The resulting coefficient was found to vary between 0.57 and 0.85 for normal clothing [14].With similar drag factors for dry and wet roadway conditions [15]. For the purpose of accident reconstruction, a drag factor of 0.7 for a clothed individual sliding on a roadway is generally accepted.
Evidence from final rest positions of the motorcycle and rider can be used to establish whether the rider was involved in a lowside or highside motorcycle ejection. In a lowside crash the motorcycle will tend to slide further than the rider. Whereas in a highside crash, the rider is ejected from the motorcycle, traveling additional distance over ground in a similar direction to the motorcycle, prior to making contact with the ground and initiating the slide. Hence, in a highside crash, the final rest position of the rider may be beyond the final rest position of the motorcycle. Furthermore, in higher-energy ejection crashes the rider is more likely to both slide and tumble, resulting in a longer travel distance from location of ejection from the motorcycle, as well as additional injuries as evidenced by fractures, lacerations and contusions to various regions of the body.
5.3. Rider anthropometry
Anthropometry is the study of human body measurements. Rider anthropometry will directly affect fall height, since head center of mass (HCOM) and overall center of mass (RCOM) varies between individuals.
In a lowside crash, seated height of the center of mass (HCOM) of the rider’s head approximates vertical fall height. Whereas in a highside crash vertical fall height is a function of seated head CoM height (HCOM), plus additional height gained based on trajectory of the rider calculated with reference to overall center of mass of the rider (RCOM) (Figure 2).
Figure 2 – Fall Height Associated with Low side and High side Accidents
5.4. Rider center of mass
Rider center of mass height (RCOM) is located anatomically with respect to the second sacral vertebra (S2), which can be visually estimated as approximate in height to the omphalion (navel), and is measured vertically with respect to the road surface. The preferred method for determining RCOM is to measure seated height of the rider on the subject motorcycle (Figure 3). If the rider is not available due to injury or fatality, then an exemplar same-gender person of similar height and weight may be used. If the subject motorcycle is not available due to extent of damage, then an exemplar motorcycle should be obtained. With the motorcycle supported perpendicular to the road by an assistant (not on side stand or center stand), and rider’s hands on the handlebar grips and feet on the foot pegs, measure the vertical height from the ground to the motorcycle seat at the location of the ischial tuberosities (base of the pelvic bones at the seat surface). An anthropometer and spirit level should ideally be used for accuracy and measurements recorded in millimeters to maximize precision.
Figure 3 – Rider anthropometry
As an alternative method, rider seated height can be calculated by sourcing motorcycle seat height, from manufacturer specifications, from which a correction factor for suspension compression under mass of the rider is subtracted. Suspension compression, also known as sag, will vary by motorcycle type and mass of the rider. A general rule of thumb is that the front sag should be about 30-35% of travel, while the rear should be at about 25%, which equates to 30-40 mm at the front and 25-35 mm at the rear for most bikes [16]. Therefore, a reasonable correction factor for suspension sag is 30-35 mm.
For both methods, an adjustment must be added to the compressed seat height to determine RCOM. According to Pheasant [17], seated RCOM is equal to seat height plus 10% of total stature (standing height). This factor calculation is identical for both males and females (Table 2).
Table 2: Anthropometric Data
5.5. Head center of mass
Head center of mass (HCOM) height can also be measured directly using the method described earlier, with the rider seated on the subject motorcycle in the correct riding position. An anthropometer is used to measure the vertical height from the ground. If the rider and/or subject motorcycle is unavailable, a substitute individual of similar height and weight and exemplar motorcycle may be used. The canthus (outer corner of the eye) is used as an anatomical landmark reference, equal in height to the center of mass of the head (Figure 3).
Alternatively, seated head center of mass (HCOM) can be calculated as a function of stature (standing height). Utilizing data from the 1988 Anthropometric Survey of U.S. Personnel [18], HCOM is derived by multiplying stature by 45.2%. Similar to the RCOM calculation, HCOM must be corrected for posture by multiplying HCOM by the cosine of seated back angle (β), measured with respect to the vertical axis.
5.6. Trajectory of the rider
The trajectory is the path that a rider is thrown or vaulted under the action of gravity, neglecting all other forces, such as friction from air resistance, without additional propulsion (Figure 4) and is defined by Equation 1.
Equation 1 – Trajectory of the ejected rider (y):
Figure 4 – Trajectory of an Ejected Rider
The following standard mathematical formulae are used to determine specific components of trajectory that are pertinent to the kinematic analysis of a rider ejected from a motorcycle.
5.7. Distance travelled
In a motorcycle accident reconstruction it may be possible to establish the actual distance of ejected travel of the rider, based upon location of ejection, typically between the end of any tire skid marks and start of gouge marks on the roadway, and location of bodily impact with the ground, identified by helmet paint transfer and/or identification of clothing fibers or body tissue on the roadway consistent with the rider. If the speed of the motorcycle at ejection (νejection) is also known, then the distance travelled (d) can be computed using the formula below, taking into account any correction factors for relative change in road height from location of ejection to impact.
Equation 2 – Horizontal distance traveled (d):
However, the location of bodily impact is often difficult to identify, in which case reasonable assumptions may be made, including utilization of an estimated ejection angle (θ).
5.8. Maximum height
One of the most critical factors for determination of total impact velocity in a motorcycle accident reconstruction is the maximum height attained by an ejected rider, which is calculated according to
Equation 3 – Maximum height (h):
5.9. Ejection angle
The ejection angle (θ) is the angle at which a rider must be launched in order to travel a certain distance, given the initial velocity. Oftentimes, based on the final rest positions of the motorcycle and rider and in consideration of appropriate drag factors, it is possible to approximate rider ejection velocity. Air resistance is considered negligible, therefore angle and velocity at ejection are considered equal to the angle and velocity at impact.
Equation 4 – Ejection angle (θ):
5.10. Rider impact velocity
Total impact velocity is derived on the basis of its vertical, angular and travel velocity components.
5.11. Linear vertical impact velocity
Vertical impact velocity is computed as a function of seated head height, plus any additional height gained due to rider ejection from the motorcycle. The potential energy (P.E.) at any point will depend on the mass (m) at that point and its distance above the ground (h), multiplied by the gravitational acceleration constant (g) (Figure 5).
Figure 5 – Potential Energy of a Motorcyclist
The potential energy of the entire system is the integral of the energies of each finite mass element of the motorcycle plus rider over its height: . For simplification, we assume that the mass is evenly distributed over the system. Hence, P.E=m g h.
In physics, the law of conservation of energy governs that energy can neither be created nor destroyed, Potential Energy (P.E.) at the start of a fall must be equal to the Kinetic Energy (K.E.) at the end of the fall, which is expressed as the product of one half mass (½m) and impact velocity squared (v2). Therefore P.E. = K.E. = ½ mv2, Solving for linear impact velocity gives Equation 5:
Equation 5 – Linear impact velocity:
5.12. Angular vertical impact velocity
In real-world scenarios a falling rider will not follow a purely linear path [19], especially when coupled to a rigid body such as a motorcycle, hence angular velocity will also be generated (Figure 6).
Figure 6 – Falling Motorcyclist
If a motorcyclist falls from a vertical to a horizontal position, we can assume that Potential Energy (P.E.) is converted to rotation: 1/2m g h = ½ I ω2 where is the Moment of inertia, defined as the ratio of the angular momentum (L) of a system to its angular velocity (ω) around an axis: I=L/w which may also be expressed in terms of its mass (m) and its distance (r) from the pivot point as: I=mr2. Since r = h, the equation can be rewritten: mgh=1/2mh2w2. Instantaneous angular velocity at impact can be expressed in terms of linear components: ν = ω h, thus mgh=1/2mv2 which yields Equation 6:
Equation 6 – Instantaneous velocity due to angular rotation upon impact:Hence total impact velocity is the sum of its linear and angular components.
Therefore, the sum of impact velocity due to linear and angular components is greater than impact velocity due to linear components only and is expressed as:
As previously stated, air resistance during a short fall is considered negligible, therefore angle and velocity at ejection (α, νejection) is considered equal to the angle and velocity at impact. Velocity due to ejection can be expressed in terms of its vertical and horizontal components . Assuming that ejection angle is measured with reference to the horizontal axis, then:
Equation 8a – Vertical ejection velocity:
, and Equation 8b – Horizontal ejection velocity:
5.14. Impact velocity vector
The impact velocity vector has both vertical and horizontal components. The total vertical velocity is the sum of the linear and angular velocity components, plus the vertical components of velocity due to ejection. The total horizontal velocity will equal the horizontal component of velocity due to ejection. The magnitude of the impact velocity vector will be the square root of the sum of its vertical and horizontal components, hence:
Equation 9 – Impact velocity vector:
and the effective angle of the impact velocity vector relative to the vertical axis is determined as:
Equation 10: Effective impact angle:
5.15. Impact acceleration
In a motorcycle accident reconstruction, impact acceleration is determined as a function of rate of change of impact velocity over time (t): , where the duration of the impact will be directly affected by the stopping distance of the impacted material. Roadside materials, such as grass or dirt inherently have larger stopping distances than typical roadway materials, such as asphalt or concrete. Hence, the impact accelerations experienced by a rider landing on a grassy area will be considerably less than if they impacted the roadway.
Motorcycle Accident Reconstruction Case Study
A cruiser motorcycle was traveling along a divided highway, approaching an intersection, when a slow-moving automobile made an abrupt unanticipated lane change immediately in front of the motorcycle. The rider applied the brakes, locking up the rear wheel, causing the motorcycle to skid. The motorcyclist swerved in an attempt to avoid contact with the automobile. The left motorcycle footplate struck the rear corner of the automobile at an impact speed of 7.2 m/s (16 mph), causing the motorcycle to rotate violently about its long axis until the tires gained traction and the rider was thrown from the motorcycle. The final resting position of the rider was 4.6 m (15 ft.) past the final resting position of the motorcycle, to which the rider slid approximately 3.7 m (12 ft.) after being vaulted approximately 6.1 m (20 ft.) from the motorcycle (Figure 7).
Figure 7 – Case study: Automobile Avoidance Collision
The rider center of mass was calculated based on anthropometric derivation from known standing height of 1.7 m (5’8”) and manufacturer’s seat height specification of 0.7 m (27.5”), from which a suspension compression factor of 30 mm (1.2”) was subtracted. Head center of mass was calculated to be 1.45 m (57”). Given a minimal back angle correction factor, based on rider position on a cruiser motorcycle, the corrected HCOM was 1.4 m (55”).
Based on the distance that the rider was thrown and given an ejection velocity of 16 mph an ejection angle of 42 degrees was computed in this motorcycle accident reconstruction. Hence, it was determined that the rider gained an additional height of 1.2 m (39”) due to ejection, which is added to the rider head center of mass height of 1.4 m (51”), for a total fall height of 2.6 m (8’6”). Using equation 7, an impact velocity of 8.0 m/s (18 mph) was calculated for the rotating fall. Since impact velocity and angle is assumed identical to ejected velocity and angle, travel velocity expressed in terms of its vertical and horizontal components, are 4.8 m/s (10.7 mph) and 5.3 m/s (11.9 mph), respectively. Therefore, the total impact velocity vertical and horizontal components are (8.0 + 4.8) = 12.8 m/s (28.7 mph) and 5.3 m/s (11.9 mph), respectively, with an effective impact angle of 22 degrees relative to the vertical axis.
The helmeted motorcyclist impacted an asphalt roadway, head first. Given the inherently very short stopping distance of such materials, the duration over which the impact velocity was experienced was very short, resulting in high impact accelerations, which produced life-threatening traumatic brain injuries.
The results computed by our motorcycle accident reconstruction model were validated by and corroborated based upon physical evidence from the accident scene as well as the physical evidence of the injuries sustained by the rider.
Conclusions
The motorcycle accident reconstruction model presented herein has been successfully applied to a typical case study involving a single motorcycle collision. Measures of rider anthropometry were incorporated into the model. In the presented motorcycle accident reconstruction case study, the rider’s stature was smaller than that of an average male and seat height was lower than most stock motorcycles. Had average male stature and average motorcycle seat height been utilized, such assumptions would have over-estimated total fall height, thereby producing a calculated vertical impact velocity greater than was actually realized. In certain circumstances, specifically where ejection angle approaches 45 degrees, a simplified model without correction for rider anthropometry and rider posture might produce results that are in disagreement with physical evidence from the accident scene. However, this improved model is not without limitations. Specifically, if a rider were leaning the motorcycle considerably at the time of loss of control, such as when cornering, the initial vertical component (yo) would be reduced. This lean angle could be estimated given the radius of the corner and if the initial speed of the motorcycle can be computed. Overall, the validation of our new motorcycle accident reconstruction model is demonstrated in its application to the motorcycle accident reconstruction case study, which is in agreement with physical evidence from the accident scene.
8. References
[1] RnR Market Research (2014) Market Research Reports Press Release: Global motorcycles market demand to rise 7.2% annually to 2016. Published July 31.
[2] National Safety Council (2013) Injury Facts – 2013 Edition. Itasca, IL..
[4] NHTSA’s National Center for Statistics and Analysis (2007) Motorcycles Traffic Safety Fact Sheet (DOT-HS-810-990), 1200 New Jersey Avenue SE, Washington, DC 20590: National Highway Traffic Safety Administration.
[5] Hurt HH, Ouellet JV, Thom DR (1981) Motorcycle Accident Cause Factors and Identification of Countermeasures. Volume 1: Technical Report. University of Southern California Traffic Safety Center, Los Angeles, CA..
[6] ACEM (2000) MAIDS (Motorcycle Accidents In Depth Study): In-depth investigations of accidents involving powered two wheelers – Final Report. European Association of Motorcycle Manufacturers, Brussels..
[7] U.S. Government Accountability Office (2012) Motorcycle Safety: Increasing Federal Funding Flexibility and Identifying Research Priorities Would Help Support States’ Safety Efforts. Report number GAO-13-42.
[9] Medwell C, McCarthy J, Shanahan M (1997) Motorcycle Slide to Stop Tests. SAE Technical Paper 970963., SP-1237 Accident Reconstruction and Animation VII, Warrendale, PA
[10] Southwestern Association of Technical Accident Investigators (1984) Motorcycle Drag Factor Tests. Phoenix, AZ.
[11] Day TD, Smith JR (1984) Friction Factor for Motorcycles Sliding on Various Surfaces. SAE paper 840250. Society of Automotive Engineers, Warrendale, PA.
[12] Iowa State Patrol (1985) Motorcycle Test Skidding on its Side, Traffic Investigation Spring Seminar. Johnston, IA..
[13] Royal Canadian Mounted Police (1984) Motorcycle Testing. Coquitlam, BC, Canada.
[14] Hague DJ (2001) Calculation of Impact Speed from Pedestrian Slide Distance. Proceedings of The Institute of Traffic Accident Investigators International Conference
[15] Searle JA, Searle A (1983) The Trajectories of Pedestrians, Motorcycles, Motorcyclists, etc., Following a Road Accident. SAE paper 831622.. Society of Automotive Engineers, Warrendale, PA.
[16] Thede P, Parks L (2010) Race Tech’s Motorcycle Suspension Bible. Motorbooks International publisher, UK. Cd s.
[17] Pheasant, S. (1998) Bodyspace. Taylor and Francis, London.
[18] Gordon CC, Churchill T, Caluser CE, Brandtmiller CB, McConville JT et al. (1989).1988 Anthropometric Survey of US Army Personnel. US Army Technical Report TR-89/044. Natick, MA.
[19] Barnett, RL (1995) The drunk, the child and the soldier – my how they fall. Triodyne Inc. Safety Bulletin. ISSN 1081-4140. Vol 2 (2).
D-IBFES. Diplomat, International Board of Forensic Engineering Sciences
Present Appointments
President Lloyd Industries, Inc. San Antonio, FL.
Research Director BRAINS, Inc., San Antonio, FL.
Past Employment
2002-2022 Courtesy Assistant Professor Department of Chemical and Biomedical Engineering, College of Engineering, University of South Florida, Tampa, FL
09/11-02/16 Director of Traumatic Brain Injury Laboratory / Program Specialist James A Haley Veterans Hospital, Tampa, FL
08/09-09/11 AssociateDirector Veterans Administration, Health Services Research and Development (HSR&D) / Rehabilitation Research and Development (RR&D) Research Center of Excellence, Tampa, FL
10/99-08/09 Director of Research Laboratories Patient Safety Center of Inquiry, James A. Haley Veterans Hospital, Tampa, FL
05/98-05/00 Director of Information Systems UTEK Corporation, Plant City, FL
06/96-10/99 ActingDirector Center for Product Ergonomics, University of South Florida, Tampa, FL
01/96-05/96 Ergonomics Laboratory Manager/ Research Ergonomist Center for Product Ergonomics, University of South Florida, Tampa, FL
07/93-01/96 Principal Ergonomist The Ergonomics Institute, Hauppauge, NY
07/92-07/93 Ergonomics /Biomechanics Consultant Biomechanics Corporation of America, Melville, NY
07/90-07/91 Research Ergonomist Liberty Mutual Research Center, Hopkinton, MA
12/88-07/90 Human Reliability Consultant R M Consultants Ltd., Warrington, Cheshire, England
Columnist for Ergonomics Intelligence Report, James Publishing, Santa Ana, CA
Book reviewer for Ergonomics In Design, Human Factors and Ergonomics Society
Journal of Rehabilitation Research and Development, Department of Veterans Affairs, Washington, DC
Applied Ergonomics, Taylor and Francis, London
Ergonomics, Taylor and Francis, London
Department of Veterans Affairs HSR&D Scientific Merit Review Committee
Department of Veterans Affairs RR&D Scientific Merit Review Committee
Natural Sciences and Engineering Research Council of Canada (NSERC), grant reviewer for federal funding agency
Applied Ergonomics Journal
National Neurotrauma Society 2016 Symposium
Journal of Safety
New England Journal of Medicine
Nebraska University Press
Journal of Forensic Sciences
Grants and Funded Research
‘Biomechanical assessment of dynamic postural sway in healthy elderly.’ Role: Co-Investigator. Sponsored by Institute for Aging. Awarded $7,500, 1996.
‘Redesigning patient handling tasks and equipment to prevent nursing back injuries.’ Role: Co-Investigator. Sponsored by Department of Veterans Affairs RR&D. Awarded $305,000, 1997.
‘Effect of wrist exposures on median nerve conduction: Pilot study.’ Role: Co-Investigator. VA RR&D. Awarded $50,000, 1997.
‘Evaluation prototype: Exam room of the future.’ Role: Co-Investigator. Sponsored by BHM Medical, Inc. and Department of Veterans Affairs. Awarded $60,000, 1998.
‘Patient Safety Center of Inquiry.’ Role: Associate Director and Co-Investigator. Sponsored by VA HSR&D. Awarded $1,500,000, 1999.
‘VISN-Wide Deployment of a Back Injury Prevention Program for Nurses: Safe Patient Handling and Movement.’ Role: Co-Investigator. Sponsored by VA HSR&D. Awarded $2.4 million, 2001.
Research Enhancement Award Program: ‘Safe Patient Mobility.’ Role: Associate Director and Co-Investigator. Sponsored by VA HSR&D. Awarded $1.1 million, 2001.
‘Development and Validation of Measurement System to Quantify Spinal Compression.’ Role: Co-Investigator.’ Sponsored by VISN8 Patient Safety Center of Inquiry. Awarded $5,000, 2001.
Research Enhancement Award Program: ‘Technology to Prevent Adverse Events in Rehabilitation.’ Role: Associate Director and Co-Investigator. Sponsored by VA RR&D. Awarded $1.35 million, 2002.
Enhancement of RR&D Research Laboratory Capabilities at the Tampa Veterans Administration Medical Center. Role: Principal Investigator. Sponsored by VA RR&D. Awarded $125,000, 2002.
‘Biomechanical assessment of wheelchair transfers toward upper extremity preservation in persons with SCI.’ Role: Co-Principal Investigator. VA RR&D. Awarded $50,000, 2002.
‘Patient Safety Center of Inquiry.’ Role: Associate Director and Co-Investigator. Sponsored by VA HSR&D. Awarded $2,000,000, 2003.
‘Development of an Instrumented Mannequin for Restraint and Control Training,’ Role: Principal Investigator. Sponsored by Department of Veterans Affairs, Office of Occupational Health and Safety. Awarded $75,000, 2003.
‘Validation of the Actiwatch as a Pain Treatment Outcome Measure.’ Role: Co-Investigator. Sponsored by VA RR&D. Awarded $200,325, 2005.
‘Folding Motorized Prone-Cart.’ Role: Co-Investigator. Sponsored by VA RR&D. Awarded $357,100, 2005.
‘Development of Force Gloves for Biomechanical Evaluation of Dynamic Patient Handling Tasks.’ Role: Co-Investigator. Sponsored by University of South Florida Patient Safety Foundation. Awarded $7,000, 2005.
‘Biomechanical Evaluation of Patient Transport Activities.’ Role: Co-Investigator. Sponsored by University of South Florida Interdisciplinary Grant Program, Dane Industries, Inc. Awarded $25,000, 2005.
Tampa VA Shared Equipment Evaluation Program. VHA. Awarded $272,000, 2005.
‘Evaluation of Assistive Transfer Devices to Preserve UE Function in SCI.’ Role: Principal-Investigator. Sponsored by VA RR&D. Awarded $474,300, 2007.
Center of Excellence: ‘Maximizing Rehabilitation Outcomes.’ Role: Associate Director. Sponsored by VA HSR&D / RR&D. Awarded $4,100,000, 2009.
‘Development of Headwear to Prevent Fall-Related Injuries in Elderly Persons.’ Role: Co-Investigator / Biomechanist. Sponsored by National Institutes of Health, Small Business Innovation Research. Awarded $1,000,000, July 2010.
‘Threats to Skin Integrity Associated with Ceiling Lift Sling Use in Persons with SCI.’ Role: Principal Investigator. Sponsored by Department of Veterans Affairs, Office of Occupational Health and Safety. $600,000, February 2011.
‘Biomechanical Evaluation of Techniques Associated with Prevention and Management of Disturbed Behavior – Phase 2’ VA Portland. Role: Principal Investigator. Awarded $60,000, February 2011.
Equipment grant for Traumatic Brain Injury program. VA RR&D. Role: Principal Investigator. Awarded $239,000, April 2011
‘Biomechanical Evaluation of Techniques Associated with Prevention and Management of Disturbed Behavior – Phase 3’ VA Portland. Role: Principal Investigator. Awarded $68,700, December 2011.
Development and Evaluation of a Sling-Less Lift System. VA RR&D. Role: Principal Investigator. Awarded $730,000. ** best proposal score in history of JAHVA
Development of Motorcycle Helmets to Protect Against Traumatic Brain Injury. CDC / NCIPC. Role: Principal Investigator. $225,000. Submitted April 2015. Not funded
Lloyd JD and Baptiste A, “Patient Handling Technologies.” In: Charney, W (ed.). Handbook of Modern Hospital Safety, second edition. Taylor and Francis 2009
Pappas IP, Del Rossi, G, Lloyd J, Gutmann J, Sackellares CJ et al. Synchronization and network measures in a concussion EEG paradigm. In Models, Algorithms and Technologies for Network Analysis. 2014.
Lee WA and Lloyd JD “Biomechanical, Epidemiologic and Forensic Considerations of Pediatric Head Injuries” In Freeman MD and Zeegers M (eds). Forensic Epidemiology: Principles and Practice. Elsevier publishers, Oxford UK. 2016.
Scientific and Medical Journal Articles (Peer Reviewed)
Lloyd JD and Kelleher, V, (2000). Patient safety center of inquiry plans effective dissemination of its findings throughout the VA. Veterans Health System Journal Aug 55–56.
Nelson A, Owen B, Lloyd JD, Fragala G, Matz M, Amato M, Bowers J, Moss-Cureton S, Ramsey G and Lentz K, (2003) Safe Patient Handling and Movement: Preventing back injury among nurses requires careful selection of the safest equipment and techniques. American Journal of Nursing 103(3): 32–43
Barrett B, Phillips S, Lloyd J, Cowan L, Friedman Y et al. (2022) Evaluation of Protective Properties of Commercially Available Medical Helmets: Are Medical Helmets Protective? Journal of Patient Safety 18 (1).
Lloyd J. (2024). Traumatic Brain Injuries in Helmeted Motorcycle Crashes.STAPP Journal / SAE (pending).
Journal Articles (Non-Peer Reviewed)
Lloyd JD: (1995) Getting Injured Employees Back to the Workplace – Return to Work Planning. Workplace Ergonomics Magazine Steven Publishing, TX
Lloyd JD: (1995) A Holistic Ergonomic Approach for Successful Return to Work. Chartered Property Casualty Underwriters Society, Malvern, PA
Lloyd JD and Gross C: (1996) Ergonomic evaluation of pen design and writing characteristics. Ergonomics Intelligence Report James Publishing, Santa Ana, CA
Lloyd JD and Gross C: (1996) Biomedical stress test for carpal tunnel syndrome. Ergonomics Intelligence Report James Publishing, Santa Ana, CA
Lloyd JD: (1996) How to correctly set up an ergonomic office workstation. Ergonomics Intelligence Report James Publishing, Santa Ana, CA
Lloyd JD: (1996) A checklist for the evaluation of ergonomic stress at computer workstations. Ergonomics Intelligence Report, James Publishing, Santa Ana, CA
Gross C, Lloyd JD and Tabler R: Ergonomic Analysis of Pen Comfort and Wrist Dynamics While Writing. Unpublished. University of South Florida, Tampa, FL
Gross C and Lloyd JD: (1997) HumanTRAC: A New Method for Rapid Product Ergonomic Assessments. Unpublished. University of South Florida, Tampa, FL
Powell-Cope G, Moore H, Kearns W, Baptiste A, Lloyd JD, Applegarth S and Nelson A. (2005). The Case for Preventing Wandering and Associated Adverse Events for Veterans with Dementia. TIPS Nov/Dec 5(6): 3
Research Basis for the Development of a Dynamic Median Nerve Stress Test. Proceedings of American Occupational Health Conference. Orlando, FL, May 16, 1997
‘Work-related carpal tunnel syndrome’. Presented at Alabama Governor’s safety and health conference. Birmingham, AL. August 29, 2000
Lloyd JD and Westhoff O. Development of an Intelligent Mannequin for Research in Safe Patient Handling and Movement. Proceedings of the Sixth Annual Safe Patient Handling and Movement Conference. Clearwater, FL, March 2, 2006
Lloyd JD. Biomechanical Evaluation of Patient Transport Technologies – a project in development. Proceedings of the Sixth Annual Safe Patient Handling and Movement conference. Clearwater, FL, March 2, 2006
Belsole RJ and Lloyd JD. Repetitive wrist movements: an adverse effect on median nerve conduction. American Society for Surgery of the Hand (ASSH). 54th Annual Meeting, 1998.
Lloyd JD and Belsole RJ. Neurovascular considerations of median nerve neuropathy and implications for clinical diagnosis. American Society for Surgery of the Hand (ASSH). 54th Annual Meeting, 1998.
Lloyd JD and Belsole RJ. Repetitive wrist movements: an adverse effect on median nerve conduction. University of South Florida Health Sciences Center Research Day, February 1999.
Lloyd JD, Nelson AL, Gross CM and Menzel N. Redesigning Patient Handling Tasks and Equipment to Prevent Nursing Back Injuries. Department of Veterans Affairs, Health Services Research and Development. 19th annual meeting, February 2001.
Lloyd JD. Repetitive Wrist Movements: Clinical Implications for Ergonomic Workplace Surveillance. International Society for Occupational Ergonomics and Safety annual meeting, June 2005.
Lloyd JD. Clinical Biomechanics of Wheelchair Transfers and Repositioning Tasks in SCI. 20th Congress of the International Biomechanics Society and 29th Annual Meeting of the American Society of Biomechanics, August 2005.
Lloyd JD and Harrow JJ. Clinical Biomechanics of Wheelchair Transfers in Spinal Cord Injury. American Paraplegic Society Annual meeting, September 2005.
Harrow JJ and Lloyd JD. Biomechanical Assessment of Pressure-Relief and Repositioning Tasks in Persons with SCI. American Paraplegic Society annual meeting, September 2005.
Lloyd JD and Harrow JJ. Clinical Biomechanics of Wheelchair Transfers in Spinal Cord Injury. American Association of SCI Nursing annual meeting, September 2005.
Harrow JJ and Lloyd JD. Biomechanical Assessment of Pressure-Relief and Repositioning Tasks in Persons with SCI. American Association of SCI Nursing annual meeting, September 2005.
Lloyd JD and Harrow JJ. Biomechanical Assessment of Independent Wheelchair Transfers in Persons with SCI. American Association of SCI Nursing annual meeting, September 2006.
Campbell RR, Lloyd JD and Gutmann J. VHA Trends in the total costs of care for the polytrauma cohort: Disproportionate impact of post-acute inpatient care. Federal Interagency Conference on Traumatic Brain Injury, 2011
Lloyd JD, Gutmann J and Arslan O. Toward Biomechanical Understanding of Brain Kinematics Associated with TBI using cadaveric specimens. Federal Interagency Conference on Traumatic Brain Injury, 2011
Lloyd JD, Gutmann J and Del Rossi G. Do Ill-Fitting Helmets Amplify the Risk of Head Injury Among Youth Football Players? – A Biomechanical Analysis, with Discussion for Applicability to Military Protection. Federal Interagency Conference on Traumatic Brain Injury, 2011
Lloyd JD, Gutmann J, Craighead J & Del Rossi G. Do Helmets Prevent Concussion? 8th Annual Conference of Blast TBI, December 2011, Tampa.
Lloyd JD, Gutmann J, Craighead J & Arslan O. Biomechanics of Blast TBI. 8th Annual Conference of Blast TBI, December 2011, Tampa.
Lloyd JD & Lee WE. Biomechanics of Inflicted Head Trauma. Presented at 4th Penn State Hershey International Conference on Pediatric Abusive Head Trauma, June 27-28, 2013, Burlington, VT.
Sackellares JC, Lloyd J & Vega D EEG of Concussive Impact in Football. Submitted to American Academy of Sports Neurology Sports Concussion meeting, July 2014. Chicago.
Lloyd J & Conidi F. Preventing Concussion in Sports – A Proposed Biomechanical Threshold. Submitted to American Academy of Sports Neurology Sports Concussion meeting, July 2014. Chicago.
Lloyd JD. Military Helmets May Provide Little Protection Against Traumatic Brain Injury. Presented at Military Health System Research Symposium, August 2014. Fort Lauderdale.
Lloyd JD & Conidi FX. Biomechanical Evaluation of Helmet Protection Against Concussion and TBI. Presented at International State-of-the-Science Meeting on the Biomedical Basis for Mild Traumatic Brain Injury (mTBI) Environmental Sensor Threshold Values. November 2014. MacLean, VA.
Lloyd JD, Sabbagh J & Dickey C. Investigating the Effects of Mild Blast Injury on TBI Symptoms and Tau Pathology. Presented at International State-of-the-Science Meeting on the Biomedical Basis for Mild Traumatic Brain Injury (mTBI) Environmental Sensor Threshold Values. November 2014. MacLean, VA.
Conidi FX and Lloyd JD. Incidence of Traumatic Brain Injury in retired NFL Players. Correlation with Diffusion Tensor MRI Imaging and Neuropsychological Testing. Annual meeting of the American Academy of Neurology. 2016.
Lloyd J. Brain Injury in Sports. North American Brain Injury Society 13th Annual Conference on Brain Injury. 2016.
Lloyd J. Biomechanics of Motorcycle Helmet Protection. National Neurotrauma Society. 2016.
Lloyd JD: Controls and displays. In: Whalley S et al: Ergonomic guidelines for the offshore oil and gas industry. R.M. Consultants Ltd., Warrington, England, 1989.
Lloyd JD: Cumulative trauma disorders of the upper extremities – Experiment report: Liberty Mutual Insurance Co., Boston, MA, 1991.
Lloyd JD: A human factors approach to the design and implementation of mobile data terminals in British Gas service engineer’s vehicles. Thesis – University of Technology, Loughborough, Leicestershire, England, 1992.
Nair C and Lloyd JD: Ergonomic assessment of the N250 flight deck. PT. Industri Pesawat Terbang Nusantara, Indonesia, 1992.
Rome D, Ratner D, Braveman K and Lloyd JD: Mannequin tutorial. In: Mannequin High – ergonomics in design. Biomechanics Corporation of America, Melville, NY, 1992.
Lloyd JD: Ergonomic assessment of risk and liability for heavy electronics manufacturing facility. Square D Company, Smyrna, TN, 1992.
Lloyd JD: AADCAS Phase II – a comprehensive anthropometry and reach study using sonic digitization techniques. Grumman Aircraft Systems, Grumman Corporation, Bethpage, NY, 1992.
Lloyd JD: Ergonomic workplace assessment for materials handling operations. Fujitsu Network Transmission Systems Inc., Richardson, TX, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for a precision electronics assembly process. Fujitsu Network Transmission Systems Inc., Richardson, TX, 1993.
Lloyd JD: Corporate ergonomics program for safety and environmental compliance. Biomechanics Corporation of America, Melville, NY, 1993.
Lloyd JD: Ergonomic assessment of risk and liability, including NIOSH lifting evaluation. Philip Morris USA, Cabarrus Manufacturing Center, NC, 1993.
Lloyd JD: Engineering Workplace Assessment. Sony Music, Carrolton, GA, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for aftermarket product manufacturing division. Allied Signal, Greenville, OH, 1993.
Lloyd JD: Wrist Stress Determination. U.S. Surgical Corporation, CT, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for heavy assembly operation. Nevamar Corporation, Odenton, MD, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for a medical laboratory. MetPath Laboratories, PA, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for an office facility. Allied Signal, RI, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for packaging and warehouse activities. Allied Signal, Jackson Facility, TN, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for furnace operators. Climax Molybdenum Company, IA, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for unskilled manufacturing tasks. Climax Molybdenum Company, Langeloth Plant, PA, 1993.
Lloyd JD: Ergonomic workplace assessment and cost benefit analysis for garment manufacturing facility. Bestop Inc. – Prepared for Ergonomics Solutions Group, 1993.
Lloyd JD: Ergonomic assessment for an aftermarket product manufacturing facility. Allied Signal, UT, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for sorting and packaging workstations. Allied Signal, Aftermarket Filter Division, NV, 1993.
Mitchell D, Nair C and Lloyd JD: Ergonomic assessment of risk and liability for a vehicle servicing facility. Salt River Project, Tempe, AZ, 1993.
Lloyd JD: Ergonomic assessment of risk and liability for paper manufacturing activities. Armstrong World Industries, Lancaster, PA, 1993.
Mitchell D, Costello K and Lloyd JD: Ergonomic assessment of risk and liability for gas construction and maintenance activities. Long Island Lighting Company, New York, NY, 1993.
Lloyd JD: EARLY Workplace Assessment for The Prevention of Musculoskeletal Injuries. Neapco Inc., Pottstown, PA, 1993.
Lloyd JD: Ergonomic Assessment of Risk and Liability for a Nursing Home. Presbyterian Manors, Topeka, KS, 1993.
Lloyd JD: EARLY Workplace Assessment for The Prevention of Musculoskeletal Injuries – Electronic Sales Presentation. Pioneer Electronics, CA, 1993.
Lloyd JD: EARLY Workplace Assessment for The Prevention of Musculoskeletal Injuries. American Honda Aftermarket Accessories Division, 1993.
Lloyd JD: Ergonomic Analysis of ‘The Upper Hand’ as a Tool for Reducing Physical Stress Caused by Shoveling Activities. Brookhaven National Laboratories, 1994.
Lloyd JD and Casar T: LILCO’s Ergonomics Initiative. Long Island Lighting Company, Gas Construction and Maintenance Division, New York, NY, 1994.
Lloyd JD: Corporate Ergonomics Program for Safety and Environmental Compliance. Nu-Kanu, Inc., Long Island, NY, 1994.
Lloyd JD: Training Manual for Ergonomics Laboratory. PT. Industri Pesawat Terbang Nusantara, Indonesia, 1994.
Lloyd JD: Ergonomic Analysis to Identify Physical Stressors in the Workplace. Parker-Hannifin Corporation / Gull, Hauppauge, NY; 1994.
Lloyd JD: Ergonomic Evaluation of a Hospital Emergency Reception Station with Recommendations for Redesign. John T. Mather Memorial Hospital, Port Jeff, NY; 1994.
Lloyd JD: Anthropometry – Designing for an International Population. United Airlines, CA; 1995.
Lloyd JD: Ergonomic Guidelines for Control Position and Configuration. United Airlines; 1995.
Krueger GP, Lloyd JD and Casar T: Ergonomic and Biomechanic Best-In-Class Assessment of Five .22 Caliber Rimfire and One .223 Cal Center fire Rifles. c/o Biomechanics Corporation of America, Melville, NY; 1995
Lloyd JD: Ph.D. Course in Human Factors Engineering. Kennedy-Western University; 1995
Lloyd JD: M.S. Course in Ergonomics. Kennedy-Western University; 1995.
Lloyd JD: Ergonomic Assessment of Occupational Risk Factors. Techalloy Company Welding Division, Baltimore, MD; 1995
Lloyd JD: Rapid Ergonomic Assessment of Cumulative Hazards – Hardware Loader and Hardware Unloader. Batesville Casket Company, Manchester, TN; 1995.
Gross C, Lloyd JD and Tabler R: Ergonomics Evaluation of Five Writing Instruments. Center for Product Ergonomics, University of South Florida; 1996
Lloyd JD: Demonstration of R&D capabilities for ergonomic evaluation of Harley-Davidson motorcycles. Harley-Davidson Motor Company, Milwaukee, WI; 1996
Patient Care Ergonomics Resource Guide: Safe Patient Handling and Movement. Patient Safety Center of Inquiry. October 2001
CD-ROM Interactive Training Program on Safe Patient Handling and Movement. VA Employee Education Service. 2002
Instrumented Mannequin for Restraint and Control Training: Final Report. VA Occupational Health, Washington, DC, January 2004
AORN Guidance Statement: Safe Patient Handling and Movement in the Perioperative Setting. AORN (Association of periOperative Registered Nurses), Denver, CO; 2007
Harrow JJ, Lloyd JD, Gironda R, Nelson A, Luther S, Schulz B, Applegarth S, Baptiste A and Cresta T. Final Report – Clinical Biomechanics of Wheelchair Transfers in Spinal Cord Injury: A Pilot Study. Report # B2900P. VA Rehabilitation Research and Development Service, Washington, DC; 2007
Lloyd, JD. Tailored Medical Helmets for Specific Patient Populations and Co-Morbidities. Patient Safety Center of Inquiry, Tampa, FL; 2012
Lloyd, JD. Biomechanical Evaluation of Safe Footwear for Institutional Patients, Considering Flooring Materials and Conditions. Patient Safety Center of Inquiry, Tampa, FL; 2012
Ferguson J, Caccese V, Lloyd J. Development of Headwear to Prevent Fall-Related Injuries in Elderly Persons. NIH grant final report. 2014.
Podium Presentations
‘Ergonomics In Action’ seminar discussing the importance of workplace ergonomics. Institute of Industrial Engineers, Chapter 76. Long Island, NY, January 1994
‘Mannequin Man-Modeling and HumanCAD Training Workshop.’ Northrop Grumman Corporation. Bethpage NY, December 1994
‘Biomechanics Evaluation and Comparison of Two Pole Climbing.’ Long Island Lighting Company, Hicksville, NY, September 1995.
‘Introduction to the Center for Product Ergonomics’ NASA Occupational Health Group, Kennedy Space Center, FL; May 1996.
‘Ergonomics Applications in Space’ Bayonet Point Hospital, FL; July 1996.
‘Beyond Bricks and Mortar – Innovations for Senior Living: Ergo-House.’ West Central Florida Area Agency on Aging conference; September 17, 1996.
‘Ergonomics in Action!’ ITESM International Conference, Mexico City; September 24, 1996.
‘Applied Ergonomics in Flightdeck Design’ ITESM International Conference, Mexico City; September 25, 1996.
‘Ergonomics Applications in Space’ Department of Environmental and Occupational Health, University of South Florida; October 1996.
‘Research Basis for the Development of a Dynamic Median Nerve Stress Test’ American Occupational Health Conference, Orlando, FL; May 16, 1997.
Grand Rounds: ‘Ergonomic applications for Spinal Cord Injury patients’ James A. Haley Veterans Hospital, Tampa, FL; May 23, 1997.
‘Product Ergonomics’ OSHA Regional Conference, Clearwater, FL; July 16, 1997.
‘Elderly falling study’. USF Institute on Aging Annual Meeting, Tampa, FL; April 24, 1998.
‘Etiology of musculoskeletal disorders’. Prevention of Musculoskeletal Injuries in Healthcare Workers: State of the Science. Tampa, FL; May 14, 1998.
‘Breakthrough research in injury prevention: What technology has to offer’. Prevention of Musculoskeletal Injuries in Healthcare Workers: State of the Science. Tampa, FL; May 15, 1998.
‘Ergonomic Risk Factors in the Workplace.’ Occupational Health and Safety Administration (OSHA), Tampa, FL; February 18, 1999.
‘Introduction to the 3D Static Strength Prediction Model’. National Aeronautical and Space Administration (NASA), Kennedy Space Center, FL; May 14, 1999.
‘How to Evaluate Ergonomic Products’. National Aeronautical and Space Administration (NASA), Kennedy Space Center, FL; May 14, 1999.
‘Repetitive wrist movements: an adverse effect on median nerve conduction’. American Society for Surgery of the Hand (ASSH). 54th Annual Meeting, Boston, MA; September 1999.
‘VA Biomechanics Research Laboratory – Virtual Tour’. James A. Haley Veteran’s Hospital, Patient Safety Center Press-Day. November 15, 1999.
‘Patient Safety Center of Inquiry – Technology Innovations Division’. US GAO. March 29, 2000.
‘Work-related carpal tunnel syndrome’. Alabama Governor’s safety and health conference. August 29, 2000.
‘Factors contributing to injuries related to patient handling’. VISN 8 PSCI Safe Patient Handling Conference. January 8-10, 2001.
‘Criteria for evaluating and selecting safe patient care equipment’. VISN 8 PSCI Safe Patient Handling conference, St. Petersburg Beach, FL; January 8-10, 2001.
‘Redesigning At Risk Tasks: A Panel Discussion., Safe Patient Handling and Movement conference. St. Petersburg Beach, FL; January 8-10, 2001.
Satellite Broadcasts on Safe Patient Handling and Movement. A two part series (4 hours) held August 2001 and repeated in November 2001. Part I includes the Ergonomic Workplace Assessment Protocol for Patient Care Areas. Part II includes Selecting the Right Equipment, Patient Assessment Criteria, Algorithms, and Use of Back Injury Resource Nurses.
‘New and Emerging Technology for Safe Patient Handling and Movement’ VISN 8 PSCI Safe Patient Handling Conference, Clearwater, FL; January 16-18, 2002.
‘Biomechanics Research Laboratory: A Virtual Tour’ VISN 8 PSCI Safe Patient Handling Conference, Clearwater, FL; January 16-18, 2002.
‘Biomechanical Evaluation of Friction Reducing Devices.’ James A. Haley Veterans Hospital Research Day, Tampa, FL; April 25, 2002.
‘Evaluation of Technology to Support Safe Patient Handling and Movement.’ Safe Patient Handling and Movement Conference, Clearwater, FL; March 4-7, 2003.
‘Ergonomic Comparison of Overhead Ceiling Lifts and Mobile Floor Lifts’ VISN 8 PSCI Safe Patient Handling Conference, Clearwater, FL; March 4-7, 2003.
‘New Directions in Technology for Safe Patient Handling and Movement’ VISN 8 PSCI Safe Patient Handling Conference, Clearwater, FL; March 4-7, 2003.
‘Clinical Applications in Rehabilitation Engineering’ University of South Florida MS Rehabilitation Engineering program July 2, 2003.
’Injury Epidemiology and Prevention’ University of South Florida MPH Program. August 9, 2003.
‘Biomechanical Assessment of Pressure-Relief and Repositioning Tasks in Persons with SCI’ AASCIN Conference, Las Vegas, NV; September 2005.
‘Biomechanical Evaluation of Patient Transport Technologies’ Safe Patient Handling and Movement Conference. St. Petersburg, FL; 2006.
‘Development of an Intelligent Mannequin for Research in Safe Patient Handling and Movement’ Safe Patient Handling and Movement Conference. St. Petersburg, FL; 2006.
‘Biomechanical Evaluation of Injury Severity Associated with Patient Falls from Bed’ Evidence-Based Falls Prevention Conference. St. Petersburg, FL; 2006.
‘Biomechanical Assessment of Independent Wheelchair Transfers in SCI’ AASCIN Conference, Las Vegas, NV; September 2006.
‘Lateral Patient Transfer using a Friction Reducing Device’. November 2006.
‘Vertical Patient Transfer using a Ceiling-mounted Full-Body Lift System’. November 2006.
‘Bed to Chair Transfer using a Powered Stand-Assist Lift’. November 2006.
‘Vertical Patient Transfer using a Floor-Based Full-Body Sling Lift’. November 2006.
‘Coefficient of Friction: The Science of Slips, Trips and Falls’. Florida Justice Association. February 2007.
‘Safe Patient Handling in Operating Rooms’. Safe Patient Handling and Movement Conference. Orlando, FL; 2008.
‘Biomechanical Evaluation of Patient Transport Tasks’. Safe Patient Handling and Movement Conference. Orlando, FL; 2008.
‘Car Transfer Technologies’. Safe Patient Handling and Movement Conference. Orlando, FL; 2008.
‘Evaluation of Friction Reducing Devices’. Safe Patient Handling and Movement Conference. Orlando, FL; 2008.
‘Biomechanical Evaluation of Protective Technologies for Fall Injury Prevention’. Evidence-Based Falls Prevention Conference. Clearwater, FL; 2008.
‘Development of Evidence- Based Algorithms for Safe Patient Handling of Orthopedic Patients’. Invited paper presentation at the Sigma Theta Tau International Honor Society of Nursing, 19th International Nursing Research Congress, Singapore. 2008. (presented on behalf of project team by M. Doheny)
Risks and solutions for safe patient handling in operating rooms. 9th Annual Safe Patient Handling and Movement Conference. Orlando. April 2009.
‘Transfer and Transport: Emerging technology and protocols for safe interdepartmental patient handling’. 9th Annual Safe Patient Handling and Movement Conference. Orlando. April 2009.
‘Helmet technology to minimize head injuries associated with falls’. 10th Annual Conference on Transforming Fall Management Prevention Practices. Clearwater, FL; May 2009.
‘Commercially available mats to prevent bed-related fall injuries’. 10th Annual Conference on Transforming Fall Management Prevention Practices. Clearwater, FL; May 2009.
‘Biomechanics of Traumatic Brain Injury’. Florida Public Defender’s ‘Life Over Death’ Annual Meeting. Naples, FL 2010
‘Technology Gaps Associated with Safe Patient Handling and Movement’. 11th Annual Safe Patient Handling and Movement Conference. Orlando. April 2011.
‘Biomechanics of Pediatric Brain Injury’. Department of Children and Families, Wildwood, FL. July 2012
‘Biomechanics of Pediatric Brain Injury’. Evidence Based Medicine and Social Investigation conference, Vancouver, Canada. August 3, 2012
‘Developing Helmet Standards and Testing Methods to Protect from Brain Injury’. Proceedings of the ASTM Symposium on Concussion in Sports. Atlanta, GA. November 20, 2012
‘Biomechanics of Pediatric Brain Injury’. Presented at Department of Office of the Public Defender, 13th Judicial Circuit, Tampa, FL. January 2013
‘Biomechanics of Inflicted Head Trauma’. Presented at 4th Penn State Hershey International Conference on Pediatric Abusive Head Trauma, June 27-28, 2013, Burlington, VT.
Lloyd J. BRAINS Researchers Reveal Deficiencies in Football Helmet Design (0060) 11th Annual Conference on Brain Injury. September 18-21, 2013. New Orleans, LA.
Lloyd J. Biomechanical Evaluation of Head Kinematics During Infant Shaking Versus Pediatric Activities of Daily Living. 11th Annual Conference on Brain Injury (0070). September 18-21, 2013. New Orleans, LA.
Lloyd J. Biomechanics of Brain Injuries Associated with Short Falls in Children (0072). 11th Annual Conference on Brain Injury. September 18-21, 2013. New Orleans, LA.
Lloyd J. Using LabVIEW to Design and Evaluate a Better Football Helmet. Tampabay LabVIEW users group meeting, May 21st, 2014. Tampa, FL.
Lloyd J. Using LabVIEW and Compact DAQ for Brain Injury Research. NI week keynote presentation, August 5th, 2014. Austin, TX.
Lloyd J. Using LabVIEW to Design and Evaluate a Better Football Helmet. NI week, August 7th, 2014. Austin, TX.
Lloyd J. Mechanisms of Head and Brain Injury. Manasota Trial Lawyers Association meeting. August 27, 2014
Lloyd JD. Biomechanics of Pediatric Head and Brain Trauma. Death is Different. February 20th, 2015. Orlando, FL.
Lloyd J. Brain Injury in Sports. North American Brain Injury Society 13th Annual Conference on Brain Injury. April 8th, 2016. Tampa, FL
Lloyd J. Biomechanical and Forensic Considerations of Pediatric Head Injury. Juvenile Law Dependency and Delinquency. Hosted by Florida Office of Criminal Conflict. Lake Mary, FL. June 8, 2017.
Lloyd J. Accident Reconstruction and Human Risk Factors in Driver-Impaired Crashes. Hosted by Florida Bar Association, Masters of DUI seminar. Fort Lauderdale, FL. April 5, 2019.
‘Biomechanical assessment and stress test of dynamic postural sway to predict falls in healthy elderly’ Research Day, James A. Haley Veteran’s Hospital, Tampa, FL; April 15, 1998.
‘Effect of wrist exposures on median nerve conduction’ Research Day, James A. Haley Veteran’s Hospital, Tampa, FL; April 15, 1998.
‘A Flick of the Wrist’. University of South Florida President’s Council fundraising dinner. Tampa, FL; September 1998.
‘Repetitive wrist movements: an adverse effect on the median nerve’. University of South Florida Health Sciences Research Day. Tampa, FL; February 25, 1999.
‘Neurovascular considerations of median nerve neuropathy and implications for clinical diagnosis’. American Society for Surgery of the Hand (ASSH). 54th Annual Meeting, Boston, MA; September 1999.
‘Safe Patient Room of the Future.’ James A. Haley Veterans Hospital Research Day, Tampa, FL; April 25, 2002.
‘Stretcher Lift Design and Prototype.’ James A. Haley Veterans Hospital Research Day, Tampa, FL; April 25, 2002.
‘Whole-Body Biomechanical Model for Dynamic Analysis of Human Motion’ James A. Haley Veterans Hospital Research Day, Tampa, FL; April 29, 2005.
‘Biomechanical Evaluation of Patient Falls from Bed’. Evidenced-Based Strategies for Patient Falls and Wandering, Clearwater, FL; May 2005.
‘Estimation, Simulation, and Experimentation of a Fall from Bed’ 8th Annual Conference on Fall Prevention Strategies, Clearwater, FL; April 2007.
‘Estimation, Simulation, and Experimentation of a Fall from Bed’ James A. Haley Veterans Hospital Research Day, Tampa, FL; May 2007.
‘Evaluation of Fall Protection and Prevention Technologies’. 8th Annual Conference on Fall Prevention Strategies. Clearwater, FL; April 2007.
‘Estimation, Simulation, and Experimentation of a Fall from Bed’. 9th Annual Conference on Fall Prevention Strategies. Clearwater, FL; April 2007.
‘Biomechanical evaluation of the LiftSeat for independent patient toileting tasks’. 9th Annual Safe Patient Handling and Movement Conference. Orlando. April 2009.
‘The effects of everyday concurrent tasks on 3D overground minimum toe clearance and gait parameters’. 10th Annual Conference on Transforming Fall Management Prevention Practices. Clearwater, FL; May 2009.
‘Impact Testing to Evaluate Materials for Head Protection Devices’. 10th Annual Conference on Transforming Fall Management Prevention Practices. Clearwater, FL; May 2009.
‘Toward a Cadeveric Biomechanical Understanding of Brain Kinematics Associated with TBI’. JAHVA Research Day, 2011
‘VHA Trends in the total costs of care for the polytrauma cohort: Disproportionate impact of post-acute inpatient care’. Federal Interagency Conference on Traumatic Brain Injury, 2011
‘Toward Biomechanical Understanding of Brain Kinematics Associated with TBI using cadaveric specimens’. Federal Interagency Conference on Traumatic Brain Injury, 2011
‘Do Ill-Fitting Helmets Amplify the Risk of Head Injury Among Youth Football Players? – a Biomechanical Analysis, with Discussion for Applicability to Military Protection’. Federal Interagency Conference on Traumatic Brain Injury, 2011
‘Do Helmets Prevent Concussion?’ 8th Annual Conference of Blast Traumatic Brain Injury, December 2011, Tampa.
‘Biomechanics of Blast TBI’. 8th Annual Conference of Blast Traumatic Brain Injury, December 2011, Tampa.
‘Tampa VA Brains Researchers Reveal Deficiencies in Helmet Design’. Military Health Systems Review Symposium. August 2013, Fort Lauderdale, FL
‘How Well Do Football Helmets Protect Against Concussion and Brain Injury? American Academy of Neurology. April 30th, 2014. Philadelphia, PA.
EEG of Concussive Impact in Football. American Academy of Sports Neurology Sports Concussion meeting, July 2014. Chicago.
Military Helmets May Provide Little Protection Against Traumatic Brain Injury. Military Health Systems Research Symposium. August 2014. Ft. Lauderdale.
Lloyd JD & Conidi FX. Biomechanical Evaluation of Helmet Protection Against Concussion and TBI. International State-of-the-Science Meeting on the Biomedical Basis for Mild Traumatic Brain Injury (mTBI) Environmental Sensor Threshold Values. November 2014. MacLean, VA.
Lloyd JD, Sabbagh J & Dickey C. Investigating the Effects of Mild Blast Injury on TBI Symptoms and Tau Pathology. International State-of-the-Science Meeting on the Biomedical Basis for Mild Traumatic Brain Injury (mTBI) Environmental Sensor Threshold Values. November 2014. MacLean, VA.
Lloyd JD & Conidi FX. Do Football Helmet Add-Ons Reduce Concussion Risk? American Academy of Neurology Annual Meeting. April 2015. Washington, DC
Conferences Attended
West Central Florida Area Agency on Aging conference; September 17, 1996.
ITESM International Conference, Mexico City; September 24, 1996.
American Occupational Health Conference, Orlando, FL; May 16, 1997.
OSHA Regional Conference, Clearwater, FL; July 16, 1997.James A. Haley Veterans Hospital Research Day, FL; April 15, 1998.
Prevention of Musculoskeletal Injuries in Healthcare Workers: State of the Science. Tampa, FL; May 15, 1998
University of South Florida Health Sciences Research Day. Tampa, FL; February 25, 1999.
Alabama Governor’s safety and health conference. August 29, 2000.
VISN 8 PSCI Safe Patient Handling Conference, St. Petersburg Beach, FL; January 8-10, 2001.
Evidenced-Based Strategies for Patient Falls and Wandering, Clearwater, FL; May 2005.
AASCIN Conference, Las Vegas, NV; September 2005.
Safe Patient Handling and Movement Conference. St. Petersburg, FL; 2006.
Evidence-Based Falls Prevention Conference. St. Petersburg, FL; 2006.
AASCIN Conference, Las Vegas, NV; September 2006.
James A. Haley Veterans Hospital Research Day, Tampa, FL; May 2007.
8th Annual Conference on Fall Prevention Strategies. Clearwater, FL; April 2007.
Florida Justice Association. February 2007.
8th Annual Safe Patient Handling and Movement Conference. Orlando, FL; 2008.
9th Annual Safe Patient Handling and Movement Conference. Orlando. April 2009.
10th Annual Conference on Transforming Fall Management Prevention Practices. Clearwater, FL; May 2009.
Florida Public Defender’s ‘Life Over Death’ Annual Meeting. Naples, FL September 2010
American Academy of Forensic Sciences meeting, Chicago, IL. February 2011.
Introduction to the STAR Helmet Rating System. Virginia Tech, Blacksburg, VA. 2011.
11th Annual Safe Patient Handling and Movement Conference. Orlando. April 2011.
James A. Haley Veterans Hospital Research Day, Tampa, FL; May 2011.
Federal Interagency Conference on Traumatic Brain Injury, 2011
8th Annual Conference of Blast Traumatic Brain Injury, Tampa, December 2011
James A. Haley Veterans Hospital Research Day, Tampa, FL; May 2012.
Evidence Based Medicine and Social Investigation conference, Vancouver, Canada. August 3, 2012
New Orleans, LA. October 13-17, 2012
Special Operation Medical Association / Blast Traumatic Brain Injury, Tampa, December 2012.
American Academy of Forensic Sciences, Washington, DC. February 2013.
4th Penn State Hershey International Conference on Pediatric Abusive Head Trauma, June 27-28, 2013, Burlington, VT.
North American Brain Injury Society 11th Annual Conference on Brain Injury. September 18-21, 2013. New Orleans, LA.
North American Brain Injury Society 26th Annual Conference on Legal Issues in Brain Injury. September 18-21, 2013. New Orleans, LA.
American Academy of Neurology 66th annual meeting. April 28-May 2, 2014. Philadelphia, PA.
American Academy of Sports Neurology Sports Concussion meeting, July 2014. Chicago.
NI week. August 3-7, 2014. Austin, TX.
Military Health Systems Research Symposium. August 2014. Fort Lauderdale, FL.
International State-of-the-Science Meeting on the Biomedical Basis for Mild Traumatic Brain Injury (mTBI) Environmental Sensor Threshold Values. November 2014. MacLean, VA.
Engineering Dynamic Corporation Accident Reconstruction Course. November 10-14. Miami, FL.
American Academy of Forensic Sciences annual meeting. February 2015. Orlando, FL.
Florida Association of Criminal Defense Lawyers. Death is Different XXI. February 2015. Orlando, FL.
SAE International, April 2015. Detroit, MI.
National SBIR conference. June 15-17. National Harbor, MD.
ASTM International F08 meeting. November, 2015. Orlando, FL
North American Brain Injury Society 13th Annual Conference on Brain Injury. April 7-9, 2016. Tampa, FL.
World Reconstruction Exposition. May 2-6, 2016. Orlando, FL
National Neurotrauma Annual Meeting. June 26-29, 2016. Lexington, KY.
ASTM International F08 meeting. November 13-18, 2016. Orlando, FL
American Academy of Forensic Sciences annual meeting. February 2017. New Orleans, LA.
Juvenile Law Dependency and Delinquency. Hosted by Florida Office of Criminal Conflict. June 8-9, 2017. Lake Mary, FL.
ARC-CSI Accident Reconstruction Conference. September 18-21. Las Vegas, NV.
IPTM Symposium on Traffic Safety. May 21-24, 2018. Orlando, FL
IPTM Symposium on Traffic Safety. June 3-6, 2019. Orlando, FL
American Society of Biomechanics Virtual Annual Conference. August 3-7, 2020.
American Academy of Forensic Sciences Virtual Annual Conference. February 15-19, 2021
IPTM Symposium on Traffic Safety. June 21-24, 2021. Orlando, FL.
Pix4D conference. October 12-13, 2022. Denver, CO.
WREX 2023. World Reconstruction Exposition. April 17-21, 2023. Orlando, FL
NHTSA Workshop on Human Subjects for Biomechanical Research, Columbus, OH. October 21, 2024
STAPP Car Crash conference, Columbus, OH. October 22-24, 2024
Teaching Activities – – Graduate Students Supervised
Robert Wilson, MS; USF Department of Electrical Engineering; 1998 – ‘Occupant trajectory determinant for vehicles equipped with airbag protection systems’
Brian Waldron, BS; USF Department of Mechanical Engineering; 2000/1 ‘Engineering evaluation and modeling of harness design in full-body sling lifts’ – served as mentor for MS thesis
Oneida Westhoff, MS; USF Department of Electrical Engineering; 2003 ‘Development of an Instrumented Mannequin for Safe Patient Handling and Movement’ – served as mentor and Professor on thesis committee
Tony Cresta, MS; USF Department of Biomedical Engineering; 2003-6 ‘Biomechanical evaluation of independent transfers and pressure relief tasks in persons with SCI’ – served as mentor and Professor on thesis committee
Sruthi Vasudev Boda, MS; USF Department of Biomedical Engineering; 2003 ‘Clinical evaluation of friction reducing devices for lateral transfer of patients’ – served as mentor and Professor on thesis committee
Roberto Guerra, BS: USF Department of Electrical Engineering; 2004 ‘Development of an Instrumented Mannequin for Personal Safety Training’
Tony Morreli, BS: USF Department of Electrical Engineering; 2004 – ‘Development of an Instrumented Mannequin for Personal Safety Training’
Bonnie Bowers, MS; USF Department of Biomedical Engineering; 2004/5 ‘Biomechanics of Injuries Associated with Falls from Bed’ – served as mentor and co-Major Professor on thesis committee
Fariba Vesali, MD; USF College of Medicine; 2004 ‘Biomechanical assessment of wheelchair transfers in persons with spinal cord injury’ – served as mentor for Medical residency program
Maria Symeonidis; USF Department of Electrical Engineering; 2004 ‘Biomechanics of Injuries Associated with Falls from Bed’
Jeffrey Harrow, PhD, MD; 2006 – served as mentor for Career Development Award
Brian Schulz, PhD; 2007 – served as mentor for Career Development Award
Shawn Applegarth, PhD (c); USF Department of Mechanical Engineering; 2006 – served as mentor for PhD dissertation in biomedical engineering
Karthick Nateson; USF Department of Biomedical Engineering; 2018-9. ‘Comparison of Laboratory and Field Data Acquisition Devices for Human Activity Recording’ – served as a mentor and Professor on thesis committee
Jason Anderson; USF Department of Biomedical Engineering; 2020. ‘Psychology / Biomechanics of Falls Down Stairs’ – mentor and Co-Professor on thesis committee.
Intellectual Property
Automotive Deceleration Indicator. Filed with USF Patents and Licensing office, 4/97.
Automotive Audible Warning (Horn) Intensity Controller. Filed with USF Patents and Licensing office, 4/97.
Determination of Occupant Trajectory in Airbag Protection Systems. Filed with USF Patents and Licensing office, 5/97.
Airbag Deployment Directional Controller. Filed with USF Patents and Licensing office, 5/97. Patent application # WO2001044026A1 published 6/2001. Full patent not pursued.
Airbag Depowerment Strategy as a Function of Impact Vector and Inertial Characteristics. Filed with USF Patents and Licensing office, 6/97.
CPE USF Trademark / Service Mark / Certification Mark for display on ergonomically superior products. Filed with USF Patents and Licensing office, 7/97.
Integrated vehicular security and personal assistance system. Filed with USF Patents and Licensing office, 10/97.
Orthotic device to improve blood circulation in the median distribution of the hand. Filed with USF Patents and Licensing office, 3/98.
Swimming pool feedback eyeball / diverter switch. Filed with USF Patents and Licensing office, 3/98.
Method for biomechanical evaluation of joint kinematics. Filed with Department of Veteran’s Affairs patents and licensing office, 11/99.
Integrated sling for patient lift manipulation. Filed with Department of Veteran’s Affairs patents and licensing office, 11/99.
Technology improvement for air-assisted lateral transfer devices. Filed with Department of Veteran’s Affairs patents and licensing office, 7/02.
Lateral Transfer Accessory. Patent awarded 10/3/06. # 7,114,203
Limb Holding Device. Filed with Department of Veteran’s Affairs patents and licensing office, 09/06.
Cerebral Stress Test for Objective Measurement of Brain Performance. Provisional Patent Application #61841612. 07/13. Full patent not pursued.
Materials and their Application for Protection from Traumatic Brain Injury. Provisional Patent Application #61943488. 02/14. Full patent not pursued.
Impact Absorbing Composite Material. Full US Patent Application. 05/14. Abandoned.
Mathematical Method for Analysis of Helmet Protection Against Head and Brain Injury – filed with US Copyright Office 10/15. Abandoned.
Biomechanics (1899) is derived from the Ancient Greek bios “life” and mēchanikē “mechanics”, to refer to the study of the mechanical principles of living organisms, particularly their movement and structure. The earliest known reference to the study of biomechanics dates back to Aristotle (384– 322 BC), who published ‘DeMotu Animalium’ (On the Motion of Animals), in which he presented the mechanical concept ‘Ground Action Force’ as a starting point to deliberate where movement comes from.
The science of biomechanics has come a long way since the days of Aristotle. Contemporary biomechanics involves the application of Newtonian mechanics to determine physical capabilities and limitations of the human body. Trauma biomechanics examines whether mechanical forces acting on and within the human body may be sufficient to cause injury. The science of biomechanics is highly accepted by the courts for the purpose of explaining the mechanical causation of injuries.
Biomechanists posses advanced knowledge of human anatomy, mathematics and physics. We use this knowledge to study failure thresholds of human tissue, bone, ligaments, blood vessels, etc. When applying this knowledge to litigation, a biomechanist will perform a reconstruction to determine the forces acting on the plaintiff during the claimed injury-causing event and relate those forces to thresholds of injury. Biomechanists and Medical Doctors serve complementary roles in the medico-legal system. However a biomechanist is uniquely qualified, based on education, training and experience, to determine injury causation.
The methods that I use in my biomechanical evaluations are similar to methods that have been employed by other researchers and are generally accepted by experts in my field. Such methods have been validated and published in peer-reviewed scientific journals.
Expert in Injury Biomechanics
Dr. John Lloyd has served as a biomechanics expert for both defense and plaintiff’s counsel on hundreds of cases throughout the United States involving automobile collisions, motorcycle accidents, trucking crash as well as slips trips and falls. Dr. Lloyd is available to travel to investigate the causes of such cases. Based on his doctorate in ergonomics with a specialization in biomechanics, Dr. Lloyd can assess whether the claimed injuries meet or exceed known biomechanical thresholds of injury.
Biomechanics Laboratory
I utilize a state-of-the-science biomechanics laboratory in my evaluations, as depicted in the following figure. This biomechanics laboratory includes various certified biofidelic mannequins, dedicated test apparatus, data acquisition hardware, software, calibrated sensor instrumentation, professional photography, and high-speed and videography equipment.
Much of my research and work focusses on biomechanical evaluation of helmets, in particular motorcycle and sports helmets, including football and ski helmets.
For helmet testing, we have a standard NOCSAE (National Operating Committee for Standards in Athletic Equipment) head drop system
However, the standard NOCSAE system only measures forces associated with linear acceleration, which are attributed with focal head injuries, such as skull fractures. This system has a rigid neck and therefore cannot measure rotational or angular accelerations, which are associated with traumatic brain injuries, such as concussion and subdural hematomas. We have a modified helmet drop test system, developed in collaboration with the University of Maine, Advanced Manufacturing Center, validation of which has been published in a peer-reviewed journal
Additionally, the biomechanics laboratory is equipped with the following resources:
Monorail head drop assembly
Twin wire guided drop system (NOCSAE)
Weighted pendulum impactor
Linear bearing table
Height-adjustable, eletromagenetically-controlled freefall drop platform
20,000N impact force plate
880lb ceiling mounted lift system
Certified biofidelic adult headforms
CRABI12 biofidelic infant mannequin
Hybrid III 3-yr old biofidelic mannequin (KSS)
National Instruments 32 channel USB-6343 X-series data acquisition system
LabView 2009 data acquisition software.
Calibrated sensors, including Kistler and PCB Piezotronics tri-axial accelerometers, MEMS triple axis digital gyroscopes, and PCB Piezotronics uni-axial and tri-axial load cells.
Selection of flooring materials, including carpeting, wood and laminates as well as concrete and wood sub-flooring surrogates
Professional still photography equipment
Normal speed and high speed (up to 1kHz) videography equipment
Dr. Lloyd’s research article “Brain Injury in Sports”, co-authored with Dr. Frank Conidi has been published in the Journal of Neurosurgery.
Please email me at DrJohnLloyd@Tampabay.RR.com if you would like to receive a full copy of the published article.
Abstract
BACKGROUND
Helmets are used for sports, military, and transportation to protect against impact forces and associated injuries. The common belief among end users is that the helmet protects the whole head, including the brain. However, current consensus among biomechanists and sports neurologists indicates that helmets do not provide significant protection against concussion and brain injuries. In this paper the authors present existing scientific evidence on the mechanisms underlying traumatic head and brain injuries, along with a biomechanical evaluation of 21 current and retired football helmets.
METHODS
The National Operating Committee on Standards for Athletic Equipment (NOCSAE) standard test apparatus was modified and validated for impact testing of protective headwear to include the measurement of both linear and angular kinematics. From a drop height of 2.0 m onto a flat steel anvil, each football helmet was impacted 5 times in the occipital area.
RESULTS
Skull fracture risk was determined for each of the current varsity football helmets by calculating the percentage reduction in linear acceleration relative to a 140-g skull fracture threshold. Risk of subdural hematoma was determined by calculating the percentage reduction in angular acceleration relative to the bridging vein failure threshold, computed as a function of impact duration. Ranking the helmets according to their performance under these criteria, the authors determined that the Schutt Vengeance performed the best overall
CONCLUSIONS
The study findings demonstrated that not all football helmets provide equal or adequate protection against either focal head injuries or traumatic brain injuries. In fact, some of the most popular helmets on the field ranked among the worst. While protection is improving, none of the current or retired varsity football helmets can provide absolute protection against brain injuries, including concussions and subdural hematomas. To maximize protection against head and brain injuries for football players of all ages, the authors propose thresholds for all sports helmets based on a peak linear acceleration no greater than 90 g and a peak angular acceleration not exceeding 1700 rad/sec2.
Please call Dr. Lloyd at 813-624-8986 or email DrJohnLloyd@Tampabay.RR.com if you would like to receive a full copy of the published article “Brain Injury in Sports”
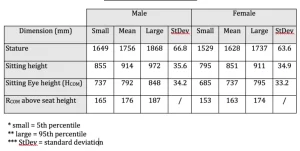
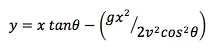
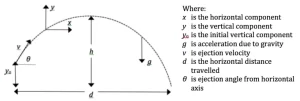
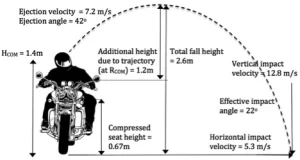
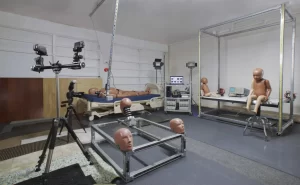
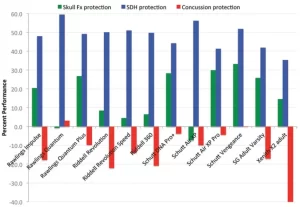
Motorcycle collision analysis is a highly specialized discipline in which Dr. Lloyd is eminently qualified as a motorcycle accident expert. In addition to holding a PhD in Ergonomics (Human Factors), with a specialization in Biomechanics, John has more that 20 years and 200,000 miles of experience riding motorcycles. Dr. Lloyd has completed numerous advanced programs, including Motorcycle Safety Foundation (MSF), Experienced Rider Course and Total Rider Tech Advanced training.
Motorcycle Helmets and Brain Injury
To consider whether a motorcycle helmet might reduce the risk of brain trauma in a motorcycle accident it is first important to understand the two primary mechanisms associated with traumatic brain injury – impact loading and impulse loading.
Impact loading involves a direct blow transmitted primarily through the center of mass of the head, resulting in extracranial focal injuries, such as contusions, lacerations and external hematomas, as well as skull fractures. Shock waves from blunt force trauma may also cause underlying focal brain injuries, such as cerebral contusions, subarachnoid hematomas and intracerebral hemorrhages. Whereas, impulse or inertial loading caused by sudden movement of the brain relative to the skull, produces cerebral concussion. Inertial loading at the surface of the brain can cause subdural hemorrhage due to bridging vein rupture, whereas if affecting the neural structures deeper within the brain can produce diffuse axonal injury (DAI).
Holbourn was the first to cite angular / rotational acceleration as an important mechanism in brain injury. Gennarelli, Thibault, and colleagues, in a series of studies using live primates and physical models investigated the role of rotational acceleration in brain injury. They concluded that angular acceleration contributes more than linear acceleration to brain injuries, including concussion, axonal injury, and subdural hematoma.
Motorcycle Helmet Testing
Traditional testing of motorcycle helmets focuses on reducing the effect of linear impact forces by dropping them from a given height onto an anvil and measuring the resultant peak linear acceleration. According to the Federal Motor Vehicle Safety Standard (FMVSS) 218, commonly known as the DOT helmet standard, the test involves dropping a motorcycle helmet onto a flat steel and hemispherical anvil at an impact velocity of 6.0 m/s (13.4mph). In general, if peak linear acceleration is less than 400g, the helmet is considered acceptable. Current motorcycle helmet testing standards do not incorporate measures of angular acceleration and therefore do not address whether any helmets can provide adequate protection against catastrophic brain injuries, such as concussion, axonal injury and subdural hematoma.
In 1995, the European Commission Directorate General for Energy and Transport initiated a Cooperative Scientific and Technical Research (COST) program to investigate Motorcycle Safety Helmets. Several agencies from Finland, the United Kingdom, France and Germany participated in this study, which compiled and analyzed data from 4,700 motorcycle fatalities in Europe, each year. The COST report documents that 75% of all fatal motorcycle accidents involve head injury. Linear forces were present in only 31% of fatal head injuries, while rotational forces were found to be the primary cause in over 60% of cases. Within the scope of this study experiments were performed using drop tests with accelerometers to measure linear and rotational accelerations of the brain and skull mass associated with different types of impacts. These tests confirmed rotational acceleration to be a primary cause of brain injury in helmeted motorcycle accidents.
Rotational forces acting on the brain are the underlying cause of traumatic brain injuries.
Motorcycle helmets, including those certified under DOT and SNELL standards are designed to mitigate forces associated with linear acceleration.
Motorcycle helmets are not currently certified under either DOT or SNELL standard against their ability to protect against the angular / rotational forces.
Epidemiologic evidence from the COST-327 report indicates that motorcycle helmets do not provide adequate protection against closed head and brain injuries
Human Factors of Motorcycle Accidents
Human factors in vehicle collisions include all factors related to drivers and other road users that may contribute to a collision. Examples include driver behavior, visual and auditory acuity, decision-making ability, and reaction speed. A 1985 report based on British and American crash data found driver error, intoxication and other human factors contribute wholly or partly to about 93% of crashes.
Motorcycle Inspection
Motorcycle accident analysis often requires involves a teardown and careful inspection of the machine to investigate for possible contributing factors. Our engineers have a combined 70 years experience with motorcycle mechanics.
A thorough evaluation includes inspection of tires, brakes, suspension setup, electrical components as well as any aftermarket parts.
Football helmet expert, Dr. John Lloyd, had the privilege to present his research on football helmets as part of the Keynote address at the National Instrument conference in Austin, TX this week. The audience of 5,000+ attendees learned about Dr. Lloyd’s research into biomechanics of the brain.
It has been said that helmets cannot prevent concussions. I disagree.
As a biomechanist I have dedicated my career to studying the biomechanics of brain injuries. There are two key mechanical forces that give rise to head and brain injuries (1) linear forces, which are responsible for visible injuries, including bruising and skull fractures, and (2) rotational forces, which cause invisible injuries, such as concussion and brain injury.
Since helmets are currently designed to pass testing standards that focus on linear forces only, it is no surprise that helmets have limited benefit in preventing concussions. Through advances in medicine we have learned that concussions can potentially have life-long neurological consequences, including memory impairement and personality changes / behavioral effects.
Over the past years I have developed and validated a testing method to evaluate helmets in terms of their ability to protect against both linear and rotational forces. Using this apparatus I characterized football helmets, results of which have been submitted to Science for publication.
Based on lessons learned from my biomechanical evaluation of various sports helmets, I have devised a matrix of shear-thickening non-Newtonian materials. A prototype helmet was constructed using this matrix liner, results of which show that rotational forces that cause concussion and other brain injuries are reduced by up to 50% compared to a leading football helmet, while also reducing linear forces.
It is my goal and my passion to work with leading helmet companies to make this technology available to players and sports participants of all aged to enhance their protection against brain trauma. I am looking to collaborate with one manufacturer in each sport to offer an exclusive license patent-pending technology.
John Lloyd of BRAINS, Inc. announced today that football head injuries and concussions can be reduced up to 50 percent with their new helmet safety breakthrough.
San Antonio, FL – Dr.John Lloyd PhD of BRAINS, Inc. announced their latest breakthrough in football helmet safety today. The unique new helmet technology promises to provide up to 50 percent more protection against football head injuries and concussions. The technology has wide application and can be used in every kind of helmet from baby helmets to military helmets, and for all athletes at risk of concussion and head injuries such as football players, cyclists, skiers, snowboarders, skateboarders, hockey players, baseball players, lacrosse players, boxers, soccer players, equestrian / horse-riding sports, such as polo and horse racing, as well as motorcycle and race car drivers.
Recent medical research documents found that concussions and cumulative head impacts can lead to lifelong neurological consequences such as chronic traumatic encephalopathy, a degenerative brain disease known as CTE and early Alzheimer’s.
The U.S. Centers for Disease Control and Prevention, estimates 1.6 – 3.8 million sport-related brain injuries annually in the United States. Of these 300,000 are attributed to youth football players, some of whom die from their injuries every year – a tragedy difficult for their mothers and families to recover from.
The severity of the issue touching both the nation’s youth and professional athletes has led to thousands of lawsuits and Congressional Hearings. Growing concern has spread to the White House where President Obama recently spoke at the Healthy Kids and Safe Sports Concussion Summit.
The BRAINS, Inc. research team, led by renowned brain injury expert, Dr. John Lloyd, has worked for years on their project to help make sports safer. A controversial subject, some opponents have stated that concussion prevention is impossible. Dedicated to saving lives and preserving brain health, Dr. Lloyd and team persevered with their work leading to this new innovation. “Our results show that forces associated with concussion and brain injury are reduced up to 50% compared to similar testing with a leading football helmet,” said Dr. John Lloyd, Research Director.
“The patent-pending matrix of non-Newtonian materials will not only benefit football, but can be utilized in all sports helmets as well as military, motorcycle and even baby helmets to improve protection and dramatically reduce the risk of brain injuries,” reported Dr. Lloyd.
The materials are inexpensive, and produce a helmet that is considerably lighter and more comfortable than a traditional helmet. Two additional applications of this new safety technology include medical flooring especially in hospitals and nursing homes or child play areas , as well as vehicle interiors.
About BRAINS, Inc.
BRAINS, Inc. located in San Antonio, Florida, is a research and development company focused on the biomechanics of brain injuries. The company was founded in 2011 by John D. Lloyd Bio, Ph.D., CPE, CBIS, Board Certified Ergonomist and Certified Brain Injury Specialist. He has also provided expert witness services nationwide for over 20 years in the fields of biomechanics, ergonomics and human factors, specializing in the biomechanics of brain injury, including sport and motorcycle helmet cases, slips and falls, motor vehicle accidents and pediatric head trauma. BRAINS, Inc. is open to licensing with manufacturers to bring this much-needed technology to market for the protection of sports participants and athletes of all ages. For additional information visit : http://drbiomechanics.com/sports-helmet-football-helmets/new-helmet-technology/ or call 813-624-8986.
A male high-school athlete was participating in a team sport when a player from the opposing team attempted a goal. The male athlete was the only obstacle between the opposing player and a winning goal. The high speed shot, taken from less than 10 feet away, impacted the male athlete directly in the groin. He immediately fell to his knees in pain. Thankfully, he was wearing an new athletic protector (known colloquially as a “jockstrap”), which should have prevented injury even at such close quarters. Dr. John Lloyd was retained to perform a biomechanical analysis athletic protector.
The athlete sat out the remainder of the game. Later that evening he became concerned as the swelling continued. The following day tests revealed that amputation of one of his testicles was medically necessary. As a young man, with his whole life ahead of him, the physical and emotional pain of losing a testicle was almost unbearable.
The young man had conducted his research before purchasing the new athletic protector. The packaging had promised comfort and protection. Why then did he sustain this life-changing injury?
Athletic protector biomechanics expert Dr. John Lloyd, was retained to evaluate a potential product liability case.
It was quickly discovered, interestingly, that there are no American Standards on the performance requirements of athletic protectors. Therefore, Dr. Lloyd devised a test method to evaluate exemplars of the subject jockstrap with comparison to models sold by other product manufacturers.
Balls were shot at various speeds from a pitching machine aimed at the athletic protectors affixed to a male mannequin. Each impact was recorded using a high-speed video camera, while Dr. Lloyd’s associate, standing behind the mannequin, measured the speed of each impact using a radar gun. A total of 70 tests were performed.
As the following high-speed video recording shows, the subject athletic protector deforms completely upon impact, providing the wearer with little, if any, protection from injury.
Several new design models also collapsed upon impact, while others cracked and broke
Fortunately, the old style jock strap with which many of us are familiar was among the few models that held up to impact and actually provided adequate protection.
Based on biomechanical analysis I concluded, to a reasonable degree of scientific certainty, that the subject athletic protector provides inadequate protection of the male genitalia from injury associated with impact from a moderate speed ball. This conclusion is based on evidence of extreme deformation of the jock strap upon direct impact from a ball.
Had the manufacturer evaluated their product under real-life conditions, as described herein, they would have learned that this product provides inadequate protection against injury to the male genitalia. Further, comparative testing of other available athletic protectors identified products that provide better protection.
The following is a case study in which biomechanics expert, Dr. John Lloyd, evaluated the risk of concussion and brain injury associated with headrest impact in rear end crashes.
Headrest Impact Test Apparatus:
In accordance with prior published test methods[1],[2],[3], a test apparatus was constructed to evaluate the biomechanical protection afforded by an exemplar automobile headrest against head and brain injuries during occipital head impacts in a simulated rear-end motor vehicle collision.
The apparatus involves a pendulum arm, attached by bearing housings to a weighted base. The upper body, including neck and head of a 50th percentile Hybrid III crash test dummy was mounted to the pendulum arm. Data acquisition was initiated by triggering an electromechanical release mechanism, allowing the mannequin to fall, under acceleration due to gravity, until the crash test dummy impacted the headrest and backrest (Figure 1).
Figure 1: Test apparatus
The fundamental elements and principles of this testing have been utilized in other laboratories. By utilizing a Hybrid III neck, the head impact tests are more realistic, causing head rotation at the axis between the head and neck, which produces measures of head and brain angular kinematics. The methods presented herein are based upon standardized test methodologies and published research.
Instrumentation
Four PCB Piezotronics tri-axial accelerometers (model # 356A01) were mounted in an X,Y,Z array at the center of mass of the Hybrid III headform, along with a tri-axial angular rate sensor produced by Diversified Technical Systems (composite Figure 2).
Figure 2: Sensor installation in Hybrid III headform
Sensor Calibration:
All sensors were calibrated by the manufacturer. Verification of calibration of the linear accelerometers was performed prior to testing using a calibration shaker. Results indicate that the sensors were operating in the specified frequency range and output (Figure 3).
Figure 3: Pre-test verification of linear accelerometer sensors
For the angular rate sensor, a simple validation method was devised in which the sensor was affixed to a digital goniometer that was rotated through a 90-degree angle. Using LabVIEW software, the integral of angular rate was computed, reflecting concurrence with the digital goniometer for all three planes of motion (Figure 4).
Figure 4: Pre-test validation of angular rate sensor calibration
Headrest Impact Testing:
The mannequin head was raised from the headrest in 2-inch increments from 2 inches to 30 inches, generating head impact speeds from 1 to 25 miles per hour. Two headrest positions were evaluated, along with two different Hybrid III necks representative of a stiff and relaxed neck (Figure 5), for a total of sixty tests.
Figure 5: Test apparatus with Hybrid III loose neck and headrest in lower position
Data Acquisition and Analysis:
Data from the analog sensors were acquired in accordance with SAE J211 [4], using a National Instruments compact DAQ data acquisition system and LabVIEW software (National Instruments, Austin, TX). The raw data was then filtered in MATLAB (The MathWorks, Natick, MA) using a phaseless eighth-order Butterworth filter with cutoff frequencies of 1650 Hz and 300Hz for the linear accelerometers and angular rate sensors, respectively.
Angular acceleration values for sagittal, coronal and axial planes were computed from the angular velocity data using the 5-point central difference by least squares method (Equation 1):
Equation 1: Five-point central difference by least squares method
Angular acceleration vales were also derived from the array of linear accelerometers, by the mathematical method documented by Padgaonkar et al [5].
Linear velocity was calculated by integrating linear acceleration. Mathematical methods were performed using Matlab to compute characteristic values from variables of interest. Figure 6, below illustrates peak linear acceleration and angular velocity associated with a 6.8 mph occipital head impact against a headrest.
Figure 6: Linear acceleration and angular velocity associated with headrest impact
It is noted that the major component of linear acceleration was in the X-axis (anterior-posterior), while the major component of angular velocity was in the sagittal plane, as expected.
Linear acceleration values were used to calculate Maximum Pressure (Equation 2), Gadd Severity Index (GSI) (Equation 3), and Head Injury Criterion (HIC15) (Equation 4).
Equation 2: Maximum Pressure
Equation 3: Gadd Severity Index
The Head Injury Criterion (HIC) is an empirical measure of impact severity describing the relationship between the linear acceleration magnitude, duration of impact and the risk of head trauma (Equation 4).
Equation 4: Head Injury Criterion
where a is resultant head acceleration, t2-t1 < 15 msec
With reference to the Figure 7, below, the HIC value is used to predict the risk of head trauma: Minor –skull trauma without loss of consciousness; nose fracture; superficial injuries Moderate – skull trauma with or without dislocated skull fracture and brief loss of consciousness. Fracture of facial bones without dislocation; deep wound(s) Critical – Cerebral contusion, loss of consciousness for more than 12 hours with intracranial hemorrhaging and other neurological signs; recovery uncertain.
Figure 7: Probability of specific head trauma level based on HIC value
Peak angular velocity was determined as the maximum angular velocity related to peak linear acceleration impact time. Angular velocity values were used to derive Maximum Principal Strain (MPS) (Equation 5), Cumulative Strain Damage Measure (CSDM) (Equation 6), and Brain Rotational Injury Criterion (BrIC) (Equation 7).
Equation 5: Maximum Principal Strain
Equation 6: Cumulative Strain Damage Measure
An analysis method validated by Takhounts [6] establishes physical injury criteria for various types of traumatic brain injury and uses Anthropomorphic Test Device (ATD) data to establish a kinematically based brain injury criterion (BrIC) for use with ATD impact testing. This method was utilized to express risk of diffuse brain injury according to the revised AIS scale [7] in terms of peak angular head kinematics, where:
Equation 7: Brain Rotational Injury Criterion
Headrest Impact Results:
A summary of key results is presented in Table a-d, below. The driver was aware of the pending impact, as he depressed the accelerator in an attempt to avoid the collision in the moments prior to the crash. In rear end collision tests involving human subjects, volunteers instinctively tensed their neck muscles as a protective response. Given that the driver anticipated the crash his neck muscles were likewise expectedly tense as an instinctive protective response. Therefore, the results most consistent with the subject case are presented in Tables a and b. Rows highlighted in green are consistent with change in velocity experienced by the driver during the subject crash.
Table a: Summary of test results – Neck – Stiff; Headrest – lower position
Table b: Summary of test results – Neck – Stiff; Headrest – upper positio
Table c: Summary of test results – Neck – Loose; Headrest – lower position
Table d: Summary of test results – Neck – Loose; Headrest – upper position
Skull Fracture
With reference to Ono 8, none of the impact tests approached the occipital skull fracture threshold of 140 g for impacts lasting longer than 7 milliseconds. Therefore, vehicle headrests provide excellent protection against acute skull fractures at impact speeds below 25 mph.
Traumatic Head Injury
With reference to Figure 7 and Tables a-d, maximum recorded HIC values were consistent with a 5 percent or less risk of moderate traumatic head injury. Whereas, the HIC value computed at impact speeds similar to the crash was only 3.4, at which the risk of minor or moderate traumatic head injury is negligible.
Mild Concussion
With reference to Figure 8 below, the risk of an occupant sustaining a mild concussion in a rear-end collision producing a change in velocity of 6.25 mph (range 5.4 to 7.2 mph) can be determined based on the following calculation: Risk AIS-1 = 31.744*ln(x) + 6.1748 (R2=0.67). The risk of and AIS-1 mild concussion, without post-concussion syndrome, in such an impact is 64.3% (range 59.7 to 68.8%).
Figure 8: Risk of mild concussion (AIS-1) associated with headrest impact
Severe Concussion
With reference to Figure 9, below, the risk of an occupant sustaining a severe concussion in a rear-end collision producing a change in velocity of 6.25 mph (range 5.4 to 7.2 mph) can be determined based on the following calculation: Risk AIS-2 = 0.198e0.234x (R2=0.85). The risk of severe concussion in such an impact is 0.85% (range 0.70 to 1.07%).
Figure 9: Risk of severe concussion (AIS-2) associated with headrest impact
Traumatic Axonal Injury:
Figure 10, below, is adapted from Margulies et al. 20 in which thresholds for axonal injury were developed and published based on mathematical modeling, animal testing and physical experiments. Results from occipital head impact against an exemplar headrest at a speed of 6.2 miles per hour are represented, indicating that rotational head and brain kinematics associated with such impact are well below scientifically-accepted thresholds for traumatic axonal injury.
Figure 10: Scientific Thresholds for Axonal Injury
Figure 11, below was generated from data presented in Tables a through d, to present the risk of traumatic axonal injury associated with head impact against an headrest.
Figure 11: Risk of traumatic axonal injury (AIS-4) associated with headrest impact
Results show that the risk of an occupant sustaining traumatic axonal injury in a rear-end collision producing a change in velocity of 6.25 mph (range 5.4 to 7.2 mph) can be determined based on the following calculation: Risk AIS-4 = 0.0271e0.2391x (R2=0.85). The risk of traumatic axonal injury in an impact of the magnitude experienced by the driver is 0.12% (range 0.10 to 0.15%).
Conclusions
Biomechanical testing of head and brain injury risk associated with occipital head impact against a headrest, in accordance with published methods, shows a significant risk (59.7 to 68.8%) of AIS-1 mild concussion, without post-concussion syndrome, in a 6.2 mph rear-end collision. However, the risk of an AIS-2 severe concussion in such an impact decreases to 0.70 to 1.07%, and the risk of traumatic axonal injury is only 0.10 to 0.15%. Moreover, the mechanical traumatic axonal injury is not consistent with a sagittal plane impact.
References
[1] Caccese V, Lloyd J, Ferguson J (2014) An Impact Test Apparatus for Protective Head Wear Testing Using a Hybrid III Head-Neck Assembly. Experimental Techniques.
[2] Lloyd J & Conidi F. (2015). Brain Injury in Sports. Journal of Neurosurgery. October.
[3] Lloyd J. (2017). Biomechanical Evaluation of Motorcycle Helmets: Protection Against Head and Brain Injuries.Journal of Forensic Biomechanics.
[4] SAE (2014) J211/1. Instrumentation for Impact Test – Part 1 – Electronic Instrumentation. Society of Automotive Engineers International, Surface Vehicle Recommended Practice, Warrendale, PA.
[5] Padgaonkar AJ, Krieger KW and King AI. Measurement of Angular Acceleration of a Rigid Body using Linear Accelerometers. J Applied Mechanics. Sept 1975.
[6] Takhounts EG, Craig MJ, Moorhouse K, McFadden J (2013) Development of Brain Injury Criteria (BrIC). Stapp Car Crash Journal 57: 243-266.
[7] Abbreviated Injury Scale (2008) Association for the Advancement of Automotive Medicine, Des Plaines, IL.
Dr. Lloyd has completed numerous advanced programs, including Motorcycle Safety Foundation (MSF), Experienced Rider Course and Total Rider Tech Advanced training.
