Biomechanical Evaluation of Motorcycle Helmets: Protection Against Head & Brain Injuries
John D. Lloyd, PhD, CPE
Tel: 813-624-8986 | Email: DrJohnLloyd@Tampabay.RR.com
* peer-reviewed and published in the Journal of Forensic Biomechanics, October 2017
** DOWNLOAD PDF FILE
Abstract
Motorcycle accident victims worldwide account for more than 340,000 fatalities annually, with the Unites States ranking 8th highest in number of motorcycle accident deaths, largely due to non-mandatory motorcycle helmet requirements for adults in a number of States. Seventy-five percent of all fatal motorcycle accidents involve head and brain injury, with rotational forces acting on the brain the primary cause of mortality. Current motorcycle helmets are reasonably effective at reducing head injuries associated with blunt impact. However, the mechanism of traumatic brain injury is biomechanically very different from that associated with focal head injury. This study was conducted to evaluate the effectiveness of current motorcycle helmets at reducing the risk of traumatic brain injuries.
Ten motorcycle helmet designs, including full-face, three-quarter and half-helmets were evaluated at an average impact velocity of 8.3 ms-1 (18.5 mph) using a validated test apparatus outfitted with a crash test dummy head and neck. Sensors at the center of mass of the headform enabled high-speed data acquisition of linear and angular head kinematics associated with impact.
Results indicate that none of the standard helmet models tested provide adequate protection against concussion and severe traumatic brain injuries at moderate impact speeds. Only one of the standard motorcycle helmet models tested provided adequate protection against skull fracture.
A new motorcycle helmet prototype, incorporating a liner constructed from a composite matrix of rate-dependent materials was tested, with comparison to standard motorcycle helmet designs, with very promising results. Knowledge learned from this study will facilitate the development of a new generation of advanced motorcycle helmets that offer improved protection against both head and brain injuries.
Keywords: biomechanics; motorcycle accident; motorcycle helmet; skull fracture; concussion; subdural hematoma; brain injury; TBI
Introduction
In developing countries motorcycles are required for utilitarian purposes due to lower prices and greater fuel economy, whereas in the developed world they are considered a luxury and used mostly for recreation. In 2016 there were more than 134 million motorcycles worldwide [1], 8.4 million of which were registered in the United States, representing 3.2% of all US registered vehicles. California, Florida and Texas were the leading states in terms of the motorcycle popularity; collectively representing 22% of all US registered motorcycles [2]. In 2011, U.S. motorcyclists travelled a total of 18.5 billion miles, which, while only 0.6% of total vehicle miles travelled, accounted for 14.6% (4,612) of U.S. traffic fatalities that year. Worldwide there are more than 340,000 motorcyclist fatalities annually, which equates to more than 28% of all road accident deaths [3]. According to the U.S. National Highway Traffic Safety Administration (NHTSA) and other reports, when compared per vehicle mile traveled with automobiles, due to their vulnerability, motorcyclists’ risk of a fatal crash is 30-35 times greater than that of a car occupant [4][5][6][7].
Two fundamental epidemiologic studies into the causation of motorcycle accidents have been conducted: the Hurt study in North America and the MAIDS study in Europe. According to the Hurt Report [8], 75 percent of collisions were found to involve a motorcycle and a passenger vehicle, while the remaining 25% were single vehicle accidents. The cause of motorcycle versus passenger vehicle collisions in 66% of accidents involves violation of the rider’s right of way due to the failure of motorists to detect and recognize motorcycles in traffic. Findings further indicate that severity of injury to the rider increases with alcohol consumption, motorcycle size and speed.
The most recent epidemiologic study to investigate motorcycle accident exposure data was conducted between 1999-2001 by a partnership of five European countries [9]. Findings show that passenger cars were again the most frequent collision partner (60%), where more than two-thirds of drivers reported that they did not see the motorcycle and more than half of all accidents involving motorcycles occurred at an intersection.
The COST report, which is an extension of the MAIDS study, documents that three-quarters (75%) of all motorcyclist deaths are a result of injury to the head and brain [10]. Linear forces were the major factor in 31% of fatal head injuries, while rotational forces were found to be the primary cause in over 60% of cases. While the helmet is considered the most effective means of rider protection [11], recent studies indicate that motorcycle helmets are only 37-42% successful in preventing fatal injury [12],[13]. By reducing peak linear forces acting on the head it was commonly believed that the risk of diffuse brain injuries, including concussion, subdural hematoma and diffuse axonal injury would also be prevented [8]. However, the biomechanical mechanisms of head and brain injuries are unique. New research shows that these mechanisms are poorly correlated [14].
Motorcycle Helmet Standards
Like most helmets, motorcycle helmets are modeled after ancient military helmets, the purpose of which is to provide protection against penetrating head injury, such as skull fracture. Whereas, all impacts have both linear and oblique components, which produce translational and tangential forces, respectively. The modern motorcycle helmet was introduced over 60 years ago [15]. Its outer shell serves as a second skull, diffusing impact forces over a larger surface area, while the inner liner compresses to minimize translational forces. However, a mechanism to mitigate tangential forces is absent. Since the liner fills the entire inner surface of the shell and is immobile, rotational inertia induced tangential forces are transmitted directly to the brain.
The likelihood of a helmeted motorcyclist sustaining impact loading injuries, such as skull fractures, can be determined by quantifying the magnitude of peak linear acceleration experienced by a test headform in response to impact. Whereas the risk of a rider suffering inertial or impulse loading injuries, such as concussion, axonal injury and intracranial hematoma can be computed based on impact-related angular kinematics at the headform center of mass [16],[17].
Unfortunately motorcycle helmet protection is not driven, for the most part, by advances in scientific knowledge, but by the need to meet applicable testing standards [18],[19]. In the United States, the governing specification is the federal motor vehicle safety standard (FMVSS) #218 [20]; the Snell Memorial Foundation also offers a voluntary standard M2015, which is a little more stringent [21]. Whereas BSI 6658 [22] and ECE 22.05 [23] have been adopted in European countries and AS/NZS 1698 accepted in Australasian countries [24]. Test protocols involve the guided fall of a helmeted headform onto steel anvils of various designs at impact velocities ranging from only 5.2 to 7.5 m/s (11-17 mph). The pass/fail criterion is based only on the helmet’s effectiveness in reducing peak linear acceleration, and thereby translational forces, in response to impact.
Impact-related angular head kinematics are not quantified under current motorcycle helmet standards, which therefore fail to assess whether helmets offer any protection against traumatic brain injuries. The omission of this critical measure of helmet performance is reflected epidemiologically in the disproportion of closed head and brain injuries in fatal motorcycle accidents [9,10].
Biomechanics of Head and Brain Injury
The two mechanisms associated with traumatic head and brain injury are impact loading and impulse loading, both of which are present in all impact events. Impact loading involves a blow directed through the center of mass of the head, resulting in translation of the head and brain. When thresholds of injury are exceeded, skull fractures [25], lacerations and contusions (bruising) to the head and underlying brain tissue may result [26]. Whereas, impulse or inertial loading is produced when an oblique impact, common to motorcycle crashes, creates tangential forces, causing head rotation. Since the brain is not rigidly attached to the inside of the skull, rotational inertia of the brain produces a mechanical strain on cerebral blood vessels, nerve fibers and brain tissue. When thresholds of injury are exceeded, nerve fibers in the brain may be damaged, producing concussion [27] and diffuse axonal injury (DAI) [28]. Blood vessels may also rupture, causing subdural hemorrhages (SDH) [29], the high mortality rate of which has motivated numerous studies of bridging vein failure properties [30],[31],[32],[33],[34],[35]. Subdural hematoma and traumatic axonal injury are frequently identified as the cause of serious injury or fatality in motorcycle accidents.
Holbourn [[36]] was the first to identify angular / rotational acceleration as the principal mechanism in brain injury. Gennarelli, Ommaya and Thibault further investigated the importance of rotational (angular) acceleration in brain injury causation, based on studies involving live primates and physical models, [28,29,[37],[38],[39], concluding that angular acceleration is far more critical than linear acceleration to the causality of traumatic brain injuries. They further isolated and investigated the unique effects of translational (linear) and inertial (angular) loading on the heads of primates [28], confirming that pure translation produces focal injuries, such as contusions and skull fractures, while rotationally induced inertial loading causes diffuse effects, including concussion and subdural hematoma. Closed head and brain injury, found in more than 60% of motorcycle accident fatalities, is due to inadequate helmet protection against impact-related angular head kinematics [10].
Skull fracture:
Ono [25] published thresholds for human skull fracture based on cadaver experiments. Twenty-five human cadaver skulls were exposed to frontal, occipital and lateral impacts. Each skull was covered with the rubber skin of a Hybrid II mannequin and filled with gelatin to accurately represent head mass. A series of 42 frontal, 36 occipital and 58 temporal blows were delivered to the suspended heads, during which linear accelerations were measured. A skull fracture threshold of 250 g for 3-millisecond impulse duration was established for frontal and occipital impacts, decreasing to 140 g for 7-millisecond impulse duration. Whereas the skull fracture threshold for lateral impacts is reported as 120 g over 3-millisecond duration, decreasing to 90 g over 7 milliseconds. Results indicate that skull fracture threshold is inversely related to impulse duration.
Concussion:
Several studies have attempted to establish biomechanical thresholds for concussion. Pellman et al. analyzed a series of video-recorded concussive impacts during NFL football games, reporting that concussive injury is possible at 45 g / 3500 rad/s2, while 5500 rad/s2 represents a 50% risk of concussive trauma [40]. Rowson and Duma, also using head injuries in America football as their model, conducted extensive laboratory and field-based biomechanical evaluations [41],[42],[43],[44]. Based on data from 62,974 sub-concussive impacts and 37 diagnosed concussions recorded using the Simbex, Inc. (Lebanon, NH) Head Impact Telemetry System (HITS), the investigators propose a concussion threshold of 104 ± 30 g and 4726 ± 1931 rad/s2.
Subdural Hematoma:
According to Gennarelli, the most common form of acute subdural hematoma (ASDH) is caused by shearing of veins that bridge the subdural space [29]. The severity of injury associated with bridging vein rupture has led to numerous studies of their mechanical properties (Lowenhielm [30-31,32], Lee and Haut [33], Meaney [34], and Depreitere [35]).
Lowenhielm tested 22 human parasagittal bridging vein samples from 11 decedents between the ages of 13 and 87 years without history of brain injury [30,31]. He hypothesized that blunt trauma to the head causes the brain to be displaced with respect to the dura, thereby stretching bridging veins and surrounding connective tissue. Based on his laboratory experiments, Lowenhielm found that maximal shear stresses occur about 7 milliseconds after impact, coinciding with bridging vein disruption. He concluded that bridging vein rupture may occur if peak angular acceleration exceeds 4500 rad/s2.
Depreitere subjected ten unembalmed human cadavers to 18 occipital impacts producing head rotation of varying magnitude and impulse duration in the sagittal plane [35]. Bridging vein ruptures, detected by autopsy, were produced in six impact tests. Findings suggest a mean tolerance level of approximately 6,000 rad/s2 for 10-millisecond impulse duration, which seems to decrease for longer impulse durations, however the confidence interval is rather broad due to the limited data set. Data from the research by Depreitere and Lowenhielm is presented in Figure 1.
Figure 1: Bridging vein failure as a function of impulse duration and peak angular acceleration (with line of best fit and 75% confidence intervals).
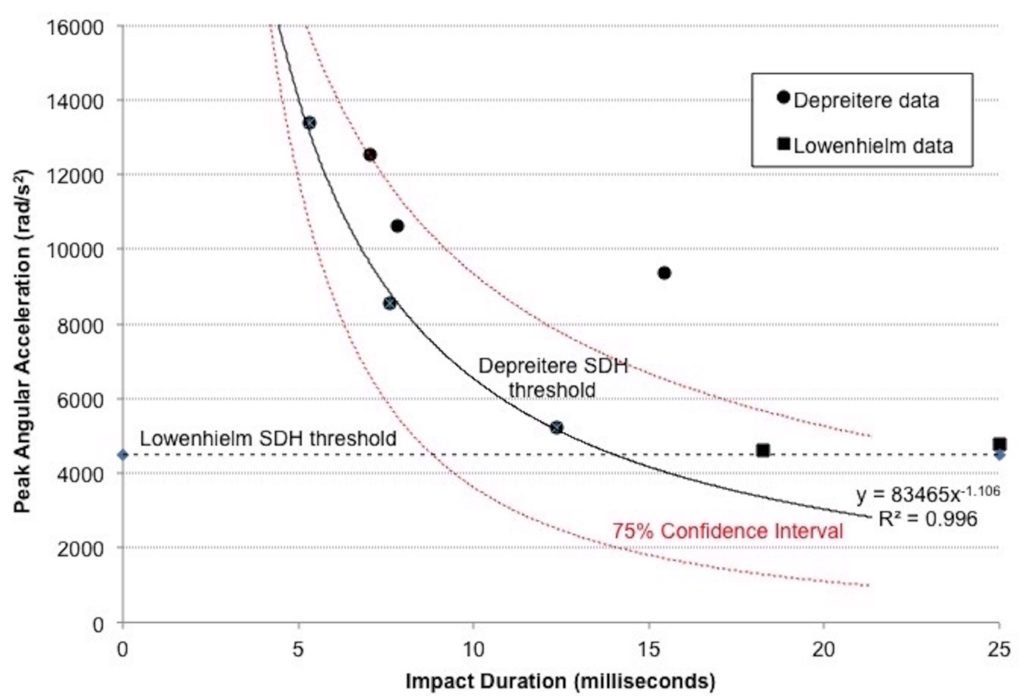 Helmets decrease peak translational force by extending the impulse duration. In the case of motorcycle helmets, typical impulse duration is approximately 12 milliseconds. With reference to Figure 1, above, this suggests that bridging vein rupture may result with peak angular accelerations in the order of 5,000 rad/s2, but may be as low as 3,000 rad/s2 after adjusting for standard error of the mean in this limited dataset.
Helmets decrease peak translational force by extending the impulse duration. In the case of motorcycle helmets, typical impulse duration is approximately 12 milliseconds. With reference to Figure 1, above, this suggests that bridging vein rupture may result with peak angular accelerations in the order of 5,000 rad/s2, but may be as low as 3,000 rad/s2 after adjusting for standard error of the mean in this limited dataset.
While previous studies have investigated motorcycle impacts into vehicles and fixed barriers, the underlying motivation of such studies was to determine crush characteristics of the vehicles for accident reconstruction purposes [45]. Other studies have evaluated peak linear accelerations of the head, chest and pelvis of motorcyclists in collisions [46]. However, rotational forces associated with impact-related peak angular accelerations have not been determined even though it is well known that rotational mechanisms are the primary cause of closed head injuries [28,29,36-37,38,39] in helmeted motorcyclist accidents [10]. Measurement of impact-related head angular / rotational acceleration is critical to the development and evaluation of motorcycle helmets to provide effective protection against traumatic brain injuries associated with a range of typical motorcycle crash-related head impact speeds. To that end, this paper offers an objective determination of the performance of a variety of motorcycle helmets in terms of their ability to protect against both head and traumatic brain injuries associated with impact velocities reflective of typical head impact velocities in motorcycle accidents.
Methods
The standard test apparatus for impact testing of protective headwear was modified to enable measurement of both linear and angular headform kinematics [16]. This validated apparatus is comprised of parallel vertical braided stainless steel wires that guide the fall of a 50th percentile Hybrid III head and neck assembly (HumaneticsATD, Plymouth, MI) mounted to an aluminum flyarm. The anvil onto which the headform impacts consists of a 50 mm thick steel base plate, with a 100 mm thick concrete overlay, consistent with the coefficient of friction for typical roadway surfaces. Figure 2 illustrates this setup.
Figure 2: Modified Head drop system with Hybrid III head / neck

According to Mellor et al. [47] apparatus for the evaluation of protective headgear in which the headform is rigidly affixed to the carriage (flyarm) reduces the dissipation of energy by excessive rotation of the helmeted headform and sliding of the helmet on the anvil, thereby inflating peak linear acceleration measures. Examples in which the headform is rigidly affixed to the flyarm include the FMVSS218 test apparatus [20]. Whereas in Snell M2015 [21], BS 6658 [22] and AS/NZS 1698 [24] specifications the headform is attached to the flyarm by means of a hinge joint, which allows headform rotation in the sagittal plane as well as vertical translation, but prevents motion in the coronal and axial planes. The ECE 22:05 test method [23] utilizes a ball joint between the flyarm and headform, thereby permitting unrestricted head rotation in all three planes. Similar to the ECE test method, utilization of the Hybrid III neck permits headform rotation in sagittal, coronal and axial planes, but limits the rate of motion in a manner more consistent with the human musculoskeletal system [48]. Moreover, orientation of the Hybrid III neck was maintained relative to the flyarm, irrespective of headform orientation, thereby standardizing response of the neck form.
Instrumentation: A triaxial block, installed at the center of mass of the Hybrid III headform (HumaneticsATD, Plymouth, MI) housed a triaxial accelerometer from PCB Piezotronics (Depew, NY) and three DTS-ARS Pro angular rate sensors (Diversified Technical Systems, Seal Beach, CA). Data from the sensors were acquired using compact DAQ hardware from National Instruments (Austin, TX).
While all sensors had been calibrated by the respective manufacturers, verification tests were performed to validate linear and angular sensor calibration data. Calibration of the tri-axial linear accelerometer was validated using a portable handheld shaker and found to be within specification for all three axes of measurement. For the angular rate sensor a simple validation method was devised in which the sensor was affixed to a digital goniometer, which was moved through a set angle (Figure 3). Using LabView, the integral of angular rate was computed, reflecting concurrence with the digital goniometer for all three planes of motion.
Figure 3: Validation of Angular Rate Sensor Calibration

Ten motorcycle helmet models were selected for evaluation, based on popularity among motorcyclists, including representative models of full-coverage, three-quarter and half-helmet (shorty) styles, as shown in Figure 4, below. All models displayed the DOT certification sticker, indicating that their protective performance met the FMVSS218 motorcycle helmet testing standard [20]. Helmet sizes were chosen based on best fit for the Hybrid III headform, which has a 58cm head circumference, representative of a 50th percentile US adult male.
Figure 4: Motorcycle Helmet Models Evaluated

In addition, a new prototype motorcycle helmet (Figure 5) was tested for comparison against the ten standard DOT motorcycle helmets. The prototype helmet was a three-quarter standard shell with liner constructed from a composite of rate-dependent materials arranged in a patent-pending matrix [49].
Figure 5: Motorcycle Helmet Prototype
 Five samples of each motorcycle helmet model were purchased in new condition. Each helmet was impacted one time in the frontal and/or occipital region at an impact velocity of approximately 8.3 meters per second (18.5 mph), which was verified computationally. Repeatability of the tests was confirmed at the start and end of data collection by dropping the Hybrid III headform from a height of 2.0 m onto a Modular Elastomer Programmer (MEP) pad of 25 mm thickness and durometer 60A. Standard Error of the Mean of 0.061 was computed based on peak angular accelerations for pre and post MEP pad drop tests.
Five samples of each motorcycle helmet model were purchased in new condition. Each helmet was impacted one time in the frontal and/or occipital region at an impact velocity of approximately 8.3 meters per second (18.5 mph), which was verified computationally. Repeatability of the tests was confirmed at the start and end of data collection by dropping the Hybrid III headform from a height of 2.0 m onto a Modular Elastomer Programmer (MEP) pad of 25 mm thickness and durometer 60A. Standard Error of the Mean of 0.061 was computed based on peak angular accelerations for pre and post MEP pad drop tests.
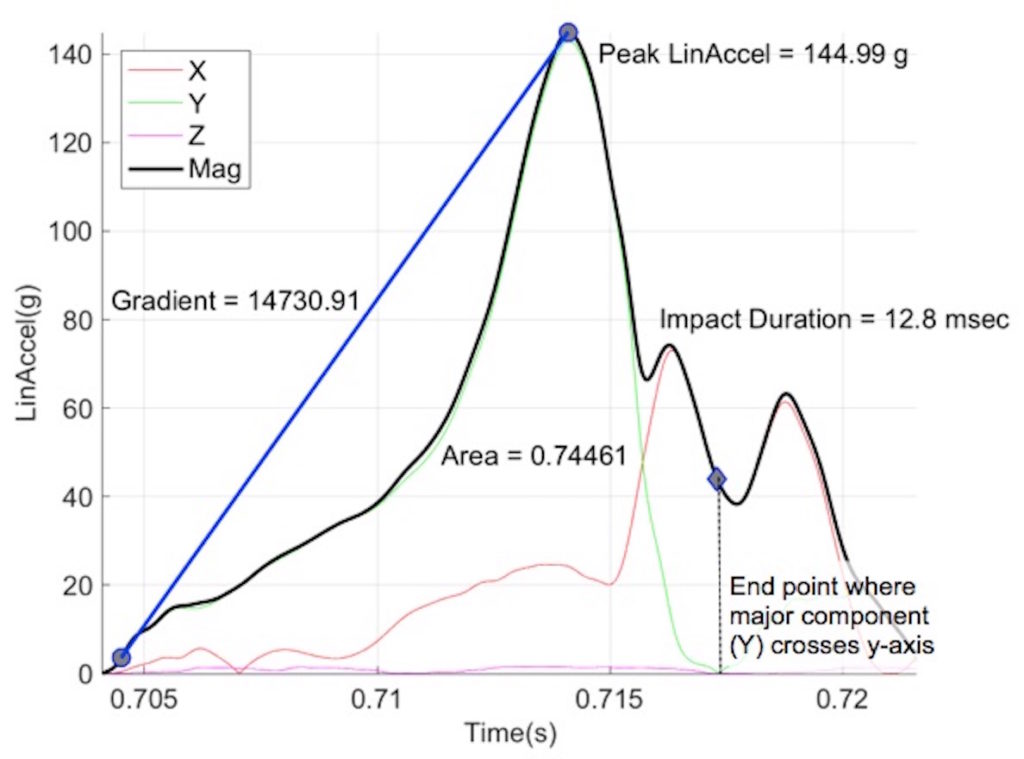
Analysis: Analog sensor data were acquired at 20 kHz per channel, in accordance with SAE J211 [50], using LabView (National Instruments, Austin, TX). The raw data was then filtered in MATLAB (The MathWorks, Natick, MA) using a phaseless eighth-order Butterworth filter with cutoff frequencies of 1650 Hz and 300Hz for the linear accelerometers and angular rate sensors, respectively. Angular acceleration measures were computed from the angular velocity data using 5-point least-squares quartic equations. Impulse duration was determined based on the linear acceleration signal, where impulse start point is the time at which the magnitude of linear acceleration exceeds 3 g and impulse end point is the time at which the major component of linear acceleration crosses the y-axis (Figure 6). The gradient from impulse start point to peak was computed, as was the area under the acceleration magnitude curve from start to end points. Variables for the angular acceleration signal were similarly computed.
Figure 6: Impulse duration based on linear acceleration data
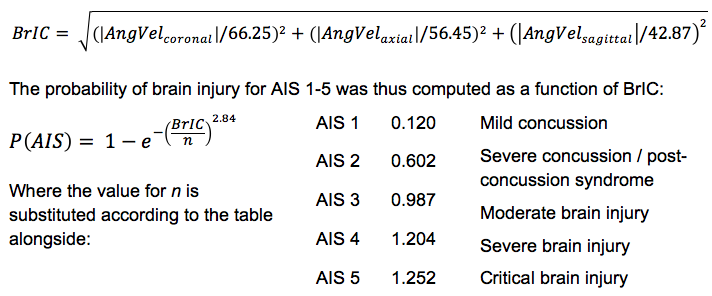
 An analysis method validated by Takhounts [51] establishes physical (strain and stress based) injury criteria for various types of brain injury based on scaled animal injury data and uses Anthropomorphic Test Device (ATD) test data to establish a kinematically based brain injury criterion (BrIC) for use with ATD impact testing. This method was utilized to express risk of brain injury according to the recently revised AIS scale [52] in terms of peak angular head kinematics, where:
An analysis method validated by Takhounts [51] establishes physical (strain and stress based) injury criteria for various types of brain injury based on scaled animal injury data and uses Anthropomorphic Test Device (ATD) test data to establish a kinematically based brain injury criterion (BrIC) for use with ATD impact testing. This method was utilized to express risk of brain injury according to the recently revised AIS scale [52] in terms of peak angular head kinematics, where:
The probability of brain injury for AIS 1-5 was thus computed as a function of BrIC:
Additionally, mechanical head and brain injury parameters of maximum pressure (in kPa), maximum principal strain (MPS) and cumulative strain damage measure (CDSM) were computed for each helmet impact test:

Results
The following table presents a summary of results for each of helmet models evaluated:
Table 1: Summary of Results
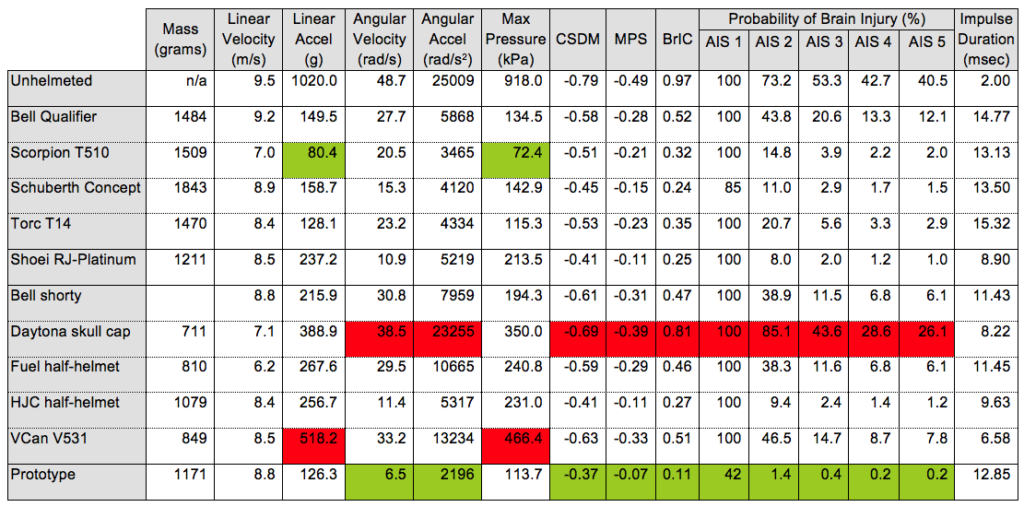
* The best performing helmet for each variable is highlighted in green
* The worst performing helmet for each variable is highlighted in red
Motorcycle Helmet Protection against Skull Fracture:
Figure 7, below, presents peak linear acceleration values, averaged across 5 samples of each of the 10 motorcycle helmet models tested, along with results for the prototype, against pass/fail thresholds for current motorcycle helmet testing standards (DOT, Snell, BS and ECE) as well as frontal-occipital and lateral skull fracture thresholds, per Ono [25].
Figure 7: Risk of Skull Fracture Associated with Motorcycle Helmet Impacts

Results show that while all of the motorcycle helmet models evaluated satisfy at least the DOT standard, only the Scorpion T510 full-face helmet offers sufficient protection against fronto-occipital and lateral impacts at the moderate impact velocities at which the helmets were tested.
Motorcycle Helmet Protection against Concussion:
Figure 8 presents peak angular acceleration results for 8.3 m/s impacts onto a concrete anvil, averaged across 5 samples of each helmet model. The red horizontal line on figure 8 indicates the 50% threshold for concussive trauma, as defined by Pellman et al [40].
Figure 8: Risk of Concussion Associated with Motorcycle Helmet Impacts
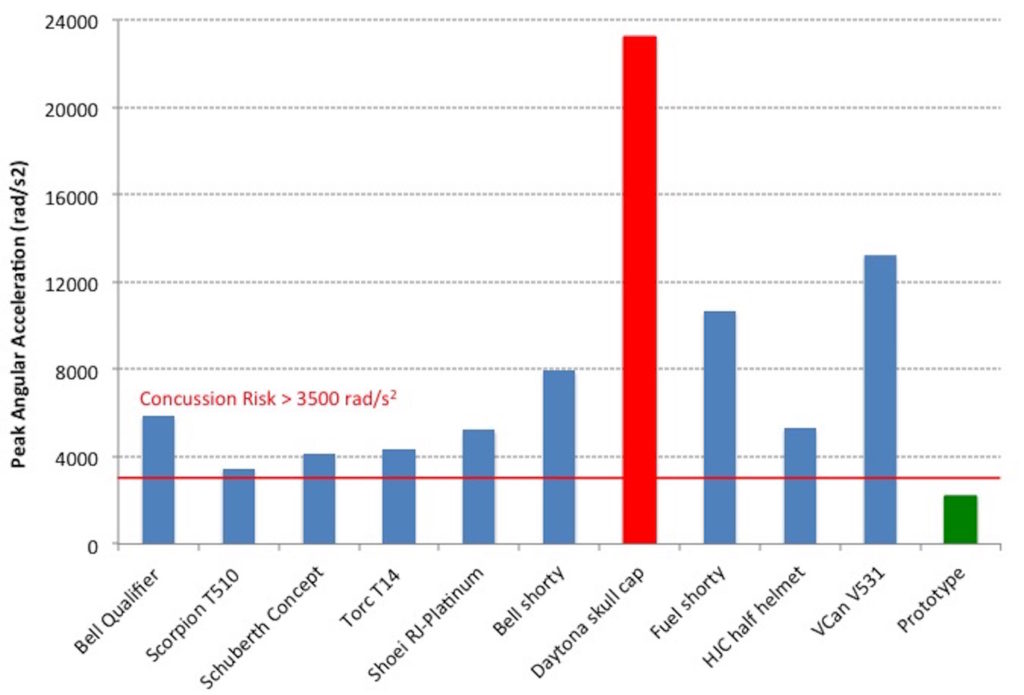
Results show that while a DOT approved motorcycle helmet may reduce peak angular acceleration associated with a helmeted head impact, the level of protection is not sufficient to prevent concussive injury in a typical motorcycle accident. Only the prototype motorcycle helmet, incorporating a liner constructed from a composite of rate-dependent materials arranged in a patent-pending matrix [49], offered adequate protection against concussive events.
Motorcycle Helmet Protection against Subdural Hematoma:
Figure 9, below, presents peak angular acceleration as a function of impulse duration, averaged across 5 samples of each of the 10 motorcycle helmet models tested, along with results for the prototype helmet. The threshold for bridging vein failure and resultant subdural hematoma is represented by the black line of best fit. Upper and lower boundary limits of this threshold are indicated in red, which represents a 75% likelihood that a subdural hematoma may occur for peak angular accelerations above the lower red line.
Figure 9: Risk of Subdural Hematoma Associated with Motorcycle Helmet Impacts
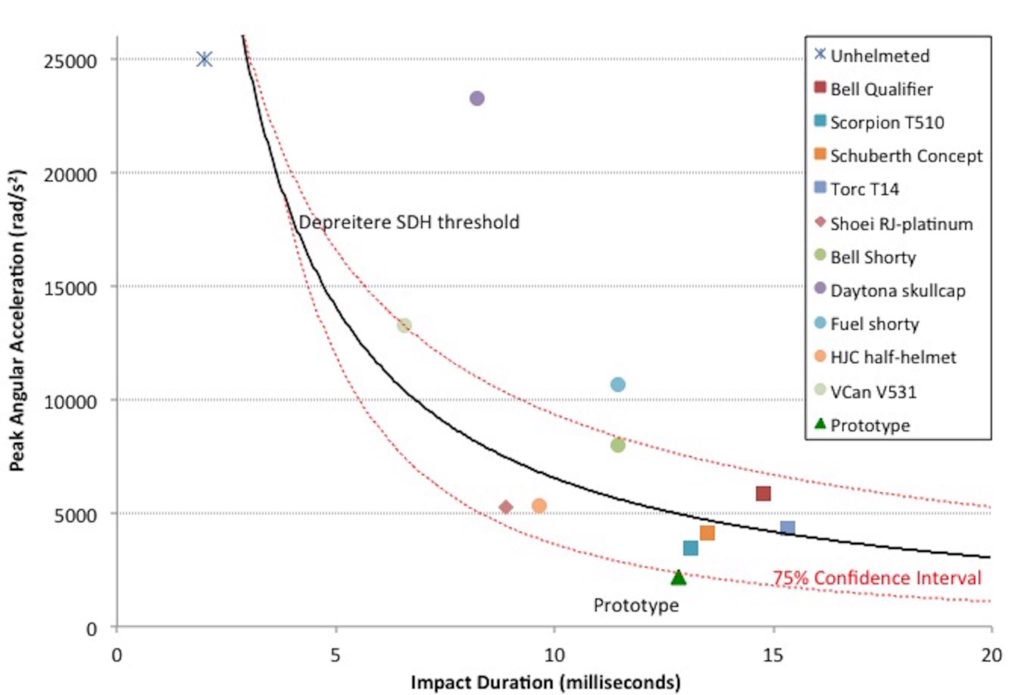
Most of the helmets tested, with exception of the prototype, fall above the lower threshold line suggesting the likelihood of catastrophic brain injury associated with a moderate helmeted impact. In fact, all but one of the five half-helmet models tested produced results above the mean threshold for subdural hematoma, indicating a higher likelihood of severe (AIS 4) or critical (AIS 5) brain injury. Overall, it appears that full-face helmets generally outperform half helmets in reducing the risk of subdural hematoma. Interestingly, an unhelmeted individual can seemingly withstand substantially greater peak angular accelerations and consequently experiences a lower risk of catastrophic brain trauma than a helmeted individual.
Correlation Analyses:
Pearson’s correlations were computed between each of the variables. Trends were suggested if computed R2 values were greater than 0.70, while strong correlations are indicated if R2 exceeded 0.80. Across all measures, the three most important variables, in rank order, for determining risk of head and brain injury are peak angular acceleration, angular acceleration gradient, and area under the angular acceleration curve between impulse start to end. The following interesting results were observed:
- A negative trend exists between helmet mass and both linear acceleration (-0.70) and angular acceleration (-0.72). That is, both peak linear acceleration and peak angular acceleration seem to decrease as helmet mass increases.
- There is neither a trend nor strong correlation between linear velocity and any of the variables investigated. This finding suggests that risk of head and brain injury is not related to impact speed.
- A strong negative correlation exists between peak linear acceleration and impulse duration (-0.92). That is, impulse duration increases as peak linear acceleration decreases.
- A trend, but not strong correlation was found between peak linear acceleration and peak angular acceleration, indicating that reducing impact-related peak linear acceleration may not necessarily mitigate peak angular acceleration.
- Peak angular acceleration is strongly correlated with rotational injury criterion (RIC36) (0.95), Brain rotational Injury Criterion (BrIC) (0.93), probability of brain injury AIS 2 through 5 (μ=0.91), angular acceleration gradient (0.98), and area under the angular acceleration curve (0.96). A strong negative correlation is identified between peak angular acceleration and cumulative strain damage measure (CSDM) (-0.94) and maximum principal strain (MPS) (-0.94). A positive trend is also noted between peak angular acceleration and maximum pressure (0.77), Gadd Severity Index (GSI) (0.74) and linear acceleration gradient (0.76).
Discussion
As presented, the mechanisms associated with causation of focal head injuries and diffuse brain injuries are very different. Helmets were originally intended and continue to be designed to reduce the risk of potentially fatal head injuries caused by skull fracture fragments penetrating the brain. While skull fractures have been almost entirely eliminated in activities such as American Football, the higher impact speeds associated with motorcycle collisions continue to result in life-threatening cranial fractures, even in areas covered by the helmet. Thus, minimizing peak linear accelerations remains an important function of any motorcycle helmet. Therefore, to minimize the risk of skull fractures associated with helmeted motorcycle collision, based on research by Ono [25], a threshold of 140 g for peak linear acceleration to the frontal and occipital areas of the head and 90 g for peak linear acceleration for lateral impacts is suggested as a suitable performance criteria.
However, as with most helmets, motorcycle helmets perform inadequately in terms of mitigating the forces responsible for causing traumatic brain injury. Though a trend may exist between peak linear acceleration and peak angular acceleration, a strong correlation is absent, consistent with prior work in this area [14]. Hence, reduced peak linear acceleration through improved helmet design may not reduce the risk of traumatic brain injury. Indeed, as results herein show, an unhelmeted individual may be at a lesser risk of subdural hematoma during a moderate speed impact than one who is wearing a DOT approved motorcycle helmet.
Motorcycle Helmet Biomechanics
To minimize the risk of traumatic brain injury, spanning from mild concussion (AIS2) through severe brain injury (AIS5), it is necessary to reduce impact-related peak angular velocities in the sagittal, coronal and axial planes. Furthermore, since risk of subdural hematoma is defined based on peak angular acceleration and impulse duration, reducing peak angular velocities while also managing impulse duration will also lend to risk reduction of such severe or critical traumatic brain injuries. Therefore, to minimize the risk of concussion and subdural hematoma in helmeted motorcycle collisions, it is suggested that performance criteria based on peak angular velocity and acceleration not exceed 15.0 rad/s and 3,000 rad/s2, respectively, as previously proposed for American Football helmets [17].
Figure 10, below, was prepared to illustrate the relative effectiveness of the ten motorcycle helmet models tested and prototype in terms of protection against skull fracture, concussion and subdural hematoma, based on the above suggested performance criteria. Results indicate that only the prototype provides adequate protection against both traumatic head and brain injuries.
Figure 10: Motorcycle Helmet Effectiveness in Protecting Against Skull Fracture, Concussion and Subdural Hematoma
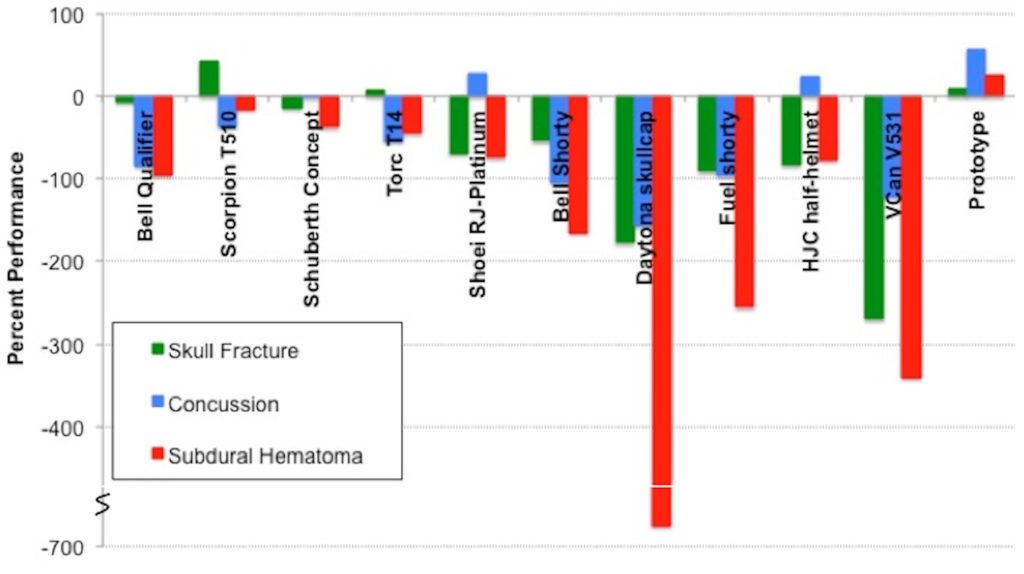
Based on the overall performance in terms of protection against skull fracture, concussion and subdural hematoma, and assuming equal weighting of these criteria for visualization purposes, the helmet models are presented in rank order in Figure 11.
Figure 11: Motorcycle Helmet Effectiveness
(presented in rank order from left to right)
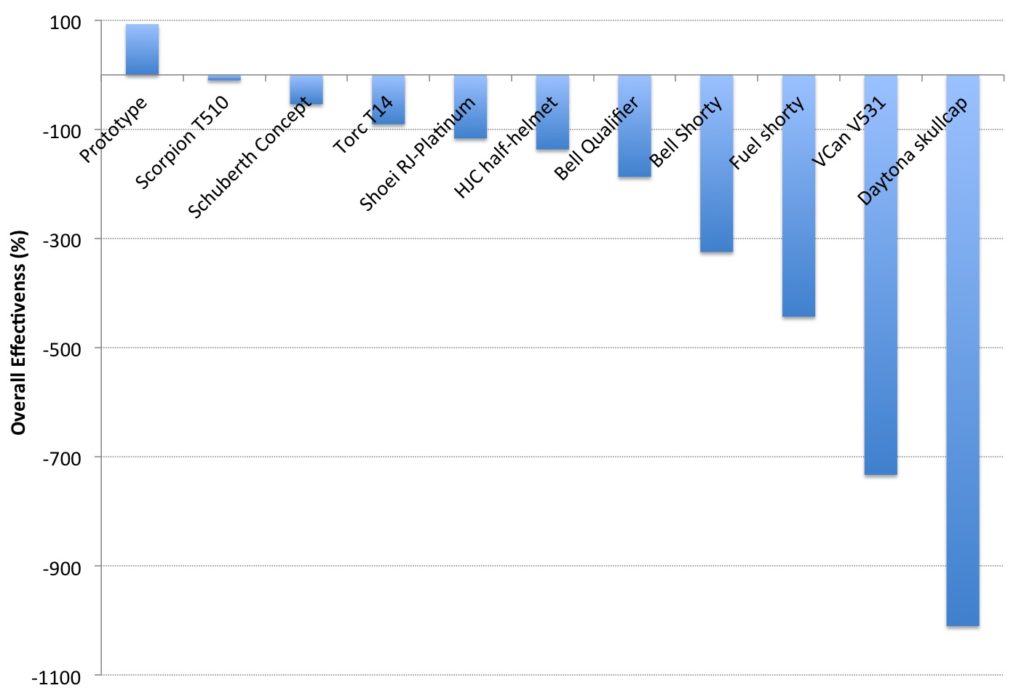
A strong negative correlation has been shown between helmet mass and both peak linear and angular accelerations. This finding suggests that ‘novelty’ motorcycle helmets (i.e. those not meeting FMVSS218 or other motorcycle helmet standards), which are often of lighter weight than DOT-approved helmets, will likely perform poorly in terms of preventing both head and brain injuries.
The new motorcycle helmet prototype evaluated within the scope of this study demonstrated exceptional potential to minimize the risk of traumatic brain injury, from mild concussion through severe brain injury, for a helmeted motorcyclist involved in a collision of moderate head impact speed.
Conclusions
The purpose of a motorcycle helmet is to reduce blunt force trauma to the head, thereby decreasing the risk of lacerations, contusions and skull fractures,. Whereas brain injuries may be produced when the brain lags behind sudden head motion thereby causing brain tissue, nerves and blood vessels to stretch and tear. The type of brain injury sustained is dependent on the magnitude and the time (pulse) duration over which mechanical stresses and strains act on the brain.
Motorcycle helmet test standards focus on reducing forces associated with linear acceleration by dropping helmeted headforms onto an anvil from a stated height and measuring the resultant peak linear acceleration. In general, the helmet design is considered acceptable if the magnitude of peak linear acceleration is less than an established threshold. Thus, helmets can and do prevent fatalities associated with penetrating head trauma. However, it may be argued that protection against brain injury is of paramount importance. After all, cuts, bruises and even bone fractures will heal, but brain injuries, if not fatal, often have life long neurologically devastating effects.
Current helmet testing standards do not require performance measures in terms of angular head kinematics and therefore fail to address whether motorcycle helmets provide the necessary protection against traumatic brain injuries. Research presented herein shows that it is possible to sustain catastrophic brain injuries, even while wearing a motorcycle helmet certified according to present testing standards.
Future generations of motorcycle helmets ought to be evaluated at higher impact velocities that are more indicative of head impact velocities in typical motorcycle accidents and should incorporate measures of both linear and angular acceleration to quantify their protective properties against both traumatic head and brain injuries.
References
[1] RnR Market Research (2014) Market Research Reports Press Release: Global motorcycles market demand to rise 7.2% annually to 2016. accessed 7/21/2017
[2] Statistica – The Statistics Portal. Number of Registered Motorcycles in the US by State. accessed 1/2/2017.
[3] WHO (2013) Road traffic injuries. Fact Sheet No. 358. The World Health Organization, Geneva.
[4] National Highway Transportation Safety Administration, Center for Statistics and Analysis (2007) NHTSA: Motorcycles Traffic Safety Fact Sheet DOT-HS-810-990. National Highway Traffic Safety Administration, Washington, DC.
[5] Lin M, & Kraus J (2008) Methodological issues in motorcycle injury epidemiology. Accident Analysis and Prevention. 40 (5): 1653–1660. PMID: 18760092
[6] Koornstra M, Broughton J, Esberger R, Glansdorp C, Koppel W, et al. (2003) Transport safety performance in the EU: a statistical overview. In: European Transport Safety Council, Brussels, Belgium.
[7] Peden M (2004) The World Report on Road Traffic Injury Prevention. World Health Organization, Geneva.
[8] Hurt HH, Ouellet JV & Thom DR (1981) Motorcycle Accident Cause Factors and Identification of Countermeasures. Volume 1: Technical Report. Traffic Safety Center, University of Southern California, Los Angeles, CA.
[9] ACEM (2009) MAIDS (Motorcycle Accidents In Depth Study): In-depth investigations of accidents involving powered two wheelers – Final Report 2.0. European Association of Motorcycle Manufacturers.
[10] Chinn B, Canaple B, Derler S, Doyle D, Otte D, et al. (2001) Cost 327, Motorcycle Safety Helmets, Final report of the action. European Commission, Directorate General for Energy and Transport, Belgium.
[11] Chang L, Chang G, Huang J, Huang S, Liu D et al. (2003) Finite Element Analysis of the effect of motorcycle helmet materials against impact velocity. Journal of the Chinese Institute of Engineers. 26: 835–843.
[12] National Highway Transportation Safety Administration (2008) Traffic Safety Facts, Data: Motorcycles. DOT HS 811 159. National Highway Traffic Safety Administration, Washington, DC.
[13] Liu B, Ivers R, Norton R, Boufous S, Blows S, Lo SK (2008) Helmets for preventing injury in motorcycle riders. Cochrane Database Syst Rev. Jan 23; (1): CD004333. PMID: 18254047
[14] Roy R (2007) Evaluation of Head Linear and Rotational Acceleration Response to Various Linear-Induced Impact Scenarios. Masters Thesis, University of Tennessee.
[15] Roth H. and Lombard C (1953) Crash helmet. US patent 2,625,683.
[16] Caccese V, Lloyd J, Ferguson J (2014) An Impact Test Apparatus for Protective Head Wear Testing Using a Hybrid III Head-Neck Assembly. Experimental Techniques. PMID: 28216804
[17] Lloyd J & Conidi F (2015) Brain Injury in Sports. Journal of Neurosurgery. 124(3):667-74 PMID: 26473777
[18] Newman J (2005) The biomechanics of head trauma and the development of the modern helmet. How far have we really come? In: Proceedings of the IRCOBI Conference, Prague.
[19] Fernandez FAO & Alves de Sousa RJ (2013) Motorcycle helmets—A state of the art review. Accident Analysis and Prevention. 56:1-21. PMID: 23583353
[20] U.S. Department of Transportation (2013) Federal Motor Carrier Safety Administration Standard No. 218, Motorcycle helmets. Washington, DC.
[21] Snell (2015) M2020 – Standard for Protective Headgear for use with Motorcycles and other motorized vehicles. Snell Memorial Foundation, North Highlands, CA.
[22] BSI (1985) BS 6658 – Specification for protective helmets for vehicle users. British Standards Institute.
[23] ECE (2002) 22.05 Protective Helmets and their Visors for Drivers and Passengers of Motorcycles and Mopeds.
[24] Australian/New Zealand Standard (2006) AS/NZS1698, Protective Helmets for Vehicle Users. Australian/New Zealand Standard.
[25] Ono K (1998) Human head impact tolerance. In Yoganandan (Ed). Frontiers in Head and Neck Trauma: Clinical and Biomechanical. IOS Press, Amsterdam.
[26] Nahum, A. M., Gatts, J. D., Gadd, C. W., Danforth, J (1993) Impact Tolerance of the Skull and Face. In Biomechanics of Impact Injury and Injury Tolerances of the Head-Neck Complex. Ed. Stanley H. Backaitis. Warrendale: Society of Automotive Engineers. 631-645.
[27] Ommaya AK, Gennarelli TA (1974) Cerebral concussion and traumatic unconsciousness. Correlation of experimental and clinical observations of blunt head injuries. Brain. 97(4): 633-54. PMID: 4215541
[28] Gennarelli TA, Thibault LE, Adams JH, Graham DI, Thompson CJ, et al (1982) Diffuse axonal injury and traumatic coma in the primate. Ann Neurol. 12(6): 564-74. PMID: 7159060
[29] Gennarelli T. and Thibault L (1982) Biomechanics of Acute Subdural Hematoma, J Trauma. 22(8), 680-686. PMID: 7108984
[30] Lowenhielm P (1974) Dynamic properties of the parasagittal bridging veins. Z. Rechtsmed. 74 (1): 55-62. PMID: 4832079
[31] Lowenhielm P (1975) Strain Tolerance of the Vv. Cerebri sup. (Bridging Veins) Calculated from Head-on Collision Tests with Cadavers. Z. Rechtsmed. 75 (2): 131-144. PMID: 4217056
[32] Lowenhielm P (1978) Tolerance level for bridging vein disruption calculated with a mathematical model. J Bioengineering. 2 (6): 501-507. PMID: 753840
[33] Lee MC and Haut RC (1989) Insensitivity of tensile failure properties of human bridging veins to strain rate: implications in biomechanics of subdural hematoma. J Biomechanics. 22 (6-7): 537–542. PMID: 2808439
[34] Meaney DF (1991) Biomechanics of acute subdural hematoma in the subhuman primate and man. University of Pennsylvania. PhD dissertation.
[35] Depreitere B, Van Lierde C, Sloten JV, Van Audekercke R, Van der Perre G, et al. (2006) Mechanics of Acute Subdural Hematoma Resulting from Bridging Vein Rupture. J Neurosurgery. 104:950–956. PMID: 16776340
[36] Holbourn AHS (1943) Mechanics of Head Injuries. The Lancet. 242(6267): 438-441.
[37] Gennarelli TA, Thibault LE, and Ommaya AK. (1972) Pathophysiologic Responses to Rotational and Translational Accelerations of the Head. SAE Technical Paper 720970.
[38] Gennarelli TA, Adams JH, Graham DI (1981) Acceleration induced head injury in the monkey I: The model, its mechanistic and physiological correlates. Acta Neuropathol. Suppl. 7:23-25. PMID: 6939241
[39] Thibault LE and Gennarelli TA (1985) Biomechanics of diffuse brain injuries. Stapp Car Crash Conference. Twenty-Ninth Proceedings, SAE Paper No. 856022, New York.
[40] Pellman EJ, Viano DC, Tucker AM, Casson IR, Waeckerle JF (2003) Concussion in professional football: reconstruction of game impacts and injuries. Neurosurgery. 53(4): 799-812. PMID: 14519212
[41] Rowson S, Brolinson G, Goforth M, Dietter D, Duma S (2009) Linear and angular head acceleration measurements in collegiate football. J Biomech Eng. 131(6). PMID: 19449970
[42] Rowson S, Goforth MW, Dietter D, Brolinson PG, Duma SM (2009) Correlating cumulative sub-concussive head impacts in football with player performance. Biomed Sci Instrum. 45:113-8. PMID: 19369749
[43] Rowson S, Duma SM, Beckwith JG, Chu JJ, Greenwald RM, et al (2012) Rotational head kinematics in football impacts: an injury risk function for concussion. Ann Biomed Eng. 40(1): 1-13. PMID: 22012081
[44] Rowson S, Duma SM (2013) Brain injury prediction: assessing the combined probability of concussion using linear and rotational head acceleration. Ann Biomed Eng. 41(5): 873-82. PMID: 23299827
[45] Adamson KS, Alexander P, Robinson EL, Johnson GM, Burkhead CI, et al. (2002) Seventeen motorcycle crash tests into vehicles and a barrier. SAE 2002-01-0551. Society of Automotive Engineers, Warrendale, PA.
[46] Severy DM, Brink HM, Blaisdell DM (1970) Motorcycle collision experiments. SAE Technical Paper 700897. Society of Automotive Engineers, Warrendale PA.
[47] Mellor AN, St Clair VJM, Chinn BP (2007) Motorcyclists’ helmets and visors – test methods and new technologies. TRL Limited, Wokingham, Berkshire, UK. Project # S0232/VF.
[48] Mertz HJ, Patrick LM (1971) Strength and Response of the Human Neck. Stapp Car Crash Conference; SAE Technical Paper 710855. Society of Automotive Engineers, Warrendale PA.
[49] Lloyd JD (2015) Impact Absorbing Composite Material. US Patents Office. US20150246502A1.
[50] SAE (2007) J211/1. Instrumentation for Impact Test – Part 1 – Electronic Instrumentation. Society of Automotive Engineers International, Surface Vehicle Recommended Practice, Warrendale, PA.
[51] Takhounts EG, Craig MJ, Moorhouse K, McFadden J (2013) Development of Brain Injury Criteria (BrIC). Stapp Car Crash Journal 57: 243-266. PMID: 24435734
[52] Abbreviated Injury Scale (2008) Association for the Advancement of Automotive Medicine, Des Plaines, IL.
